29 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 14

Câu 1:

Tập nghiệm của phương trình $x^{2} - 5 x + 6 = 0$ là

A. $\{1; 6\}$

B. $\{- 6; - 1\}$

C. $\{- 3; 2\}$

D. $\{2; 3\}$

Xem đáp án

Chọn đáp án A

Câu 2:

Điều kiện của x để biểu thức $\sqrt{2 x - 4}$ có nghĩa là

A. $x \geq \frac{1}{2}$

B. $x \geq - \frac{1}{2}$

C. $x \geq 2$

D. $x \geq - 2$

Xem đáp án

Chọn đáp án C

Câu 3:

Trên đường tròn (O) lấy các điểm phân biệtA, B, C sao cho $\hat{A O B} = 114^{0}$ (như hình vẽ bên dưới). Số đo của $\hat{A C B}$ bằng

Trên đường tròn (O) lấy các điểm phân biệt A, B, C sao cho góc AOB= 114 độ (như hình vẽ bên dưới). Số đo của góc ACB bằng (ảnh 1)

$A {.76}^{0}$

$B {.57}^{0}$

C. $38^{0}$

D. $114^{0}$

Xem đáp án

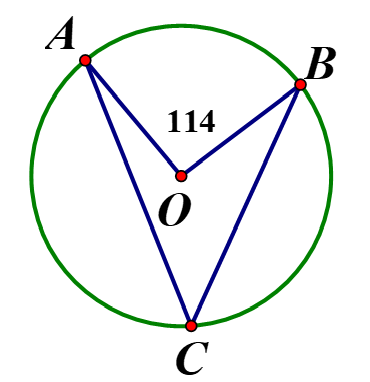
Chọn đáp án B

Câu 4:

Bạn Thanh trình bày lời giải hệ phương trình $\{\begin{cases} x - 3 y = - 3 \\ 3 x + 2 y = 13 \end{cases}$ theo các bước như sau:

*Bước 1: Hệ phương trình đã cho tương đương với $\{\begin{cases} - 3 x + 9 y = 9 \\ 3 x + 2 y = 13 \end{cases}$

*Bước 2: Cộng từng vế hai phương trình của hệ ta được: $11 y = 22 \Rightarrow y = 2$

*Bước 3: Thay $y = 2$ vào phương trình thứ nhất của hệ ta được x=3

*Bước 4: Vậy nghiệm của hệ phương trình đã cho là $(3; 2)$

Số bước giải đúng trong lời giải của bạn Thanh là:

A.1

B. 4

C. 3

D. 2

Xem đáp án

Chọn đáp án D

Câu 5:

Diện tích của một hình tròn có bán kính bằng 4cm là:

A. $64 π c m^{2}$

B. $8 π c m^{2}$

C. $4 π c m^{2}$

D. $16 π c m^{2}$

Xem đáp án

Chọn đáp án D

Câu 6:

Nghiệm của hệ phương trình $\{\begin{cases} 2 x + 3 y = 5 \\ 3 x - 2 y = - 12 \end{cases}$ là:

A. $(\frac{- 46}{5}; \frac{39}{5})$

B. $(\frac{46}{13}; \frac{- 9}{13})$

C. $(- 2; 3)$

D. $(2; - 3)$

Xem đáp án

Chọn đáp án A

Câu 7:

Thể tích của một hình cầu có bán kính bằng 15cm là

A. $4500 π c m^{3}$

B. $225 π c m^{3}$

C. $100 π c m^{3}$

D. $300 π c m^{3}$

Xem đáp án

Chọn đáp án D

Câu 8:

Cho hàm số $y = a x^{2}$ có đồ thị như hình vẽ bên dưới

Hàm số đó là

A. $y = 2 x^{2}$

B. $y = x^{2}$

C. $y = - x^{2}$

D. $y = - 2 x^{2}$

Xem đáp án

Chọn đáp án C

Câu 9:

Giá trị rút gọn của biểu thức

P = 2 \sqrt{27} + \sqrt{300} - 3 \sqrt{75}

bằng

A. $- 3 \sqrt{3}$

B. $31 \sqrt{3}$

C. $\sqrt{3}$

D. $8 \sqrt{3}$

Xem đáp án

Chọn đáp án B

Câu 10:

Điểm nào sau đây là giao điểm của đường thẳng $(d) : y = 2 x + 3$ và parabol $(P) : y = - \frac{1}{4} x^{2}$

A. $Q (6; - 9)$

B. $N (- 2; - 6)$

C. $P (- 6; 9)$

D. $M (- 2; - 1)$

Xem đáp án

Chọn đáp án B

Câu 11:

Xét hai đường tròn bất kỳ có tâm không trùng nhau $(O_{1}, R_{1}), (O_{2}, R_{2})$ và $R_{1} > R_{2} .$ Khẳng định nào sau đây sai

A. Nếu hai đường tròn tiếp xúc nhau thì $O_{1} O_{2} = R_{1} - R_{2}$

B. Nếu hai đường tròn ở ngoài nhau thì

O_{1} O_{2} < R_{1} + R_{2}

C. Nếu hai đường tròn cắt nhau thì $O_{1} O_{2} > R_{1} - R_{2}$

D. Nếu hai đường tròn tiếp xúc ngoài thì $O_{1} O_{2} = R_{1} + R_{2}$

Xem đáp án

Chọn đáp án C

Câu 12:

Cho hàm số $y = a x - 2$ có đồ thị là đường thẳng (d) như hình vẽ bên dưới. Hệ số góc của đường thẳng (d) bằng

A. 3

B. -3

C. 2

D. 1

Xem đáp án

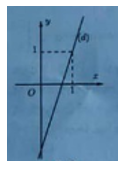
Chọn đáp án B

Câu 13:

Gọi $x_{1}, x_{2}$ là hai nghiệm của phương trình $3 x^{2} + 12 x - 14 = 0.$ Giá trị của biểu thức $T = x_{1} + x_{2}$ bằng:

A. $- \frac{14}{3}$

B. $\frac{14}{3}$

C. -4

D. 4

Xem đáp án

Chọn đáp án D

Câu 14:

Cho đường thẳng (d) cắt đường tròn (O) tại hai điểm phân biệt A,B Biết khoảng cách từ điểm O đến đường thẳng d bằng 8 cm và độ dài đoạn thẳng AB bằng 12cm Bán kính của đường tròn (O) bằng:

A. 10cm

B. $4 \sqrt{13} c m$

C. 20cm

D. $4 \sqrt{5} c m$

Xem đáp án

Chọn đáp án C

Câu 15:

Hàm số nào sau đây là hàm số bậc nhất

A. $y = \frac{2}{x} + 1$

B. $y = - 3 \sqrt{x} + 2$

C. $y = 3 x^{2}$

D. $y = 2 x - 3$

Xem đáp án

Chọn đáp án A

Câu 16:

Anh Bình đứng tại vị trí A cách một đài kiểm soát không lưu 50m và nhìn thấy đỉnh C của đài này dưới một góc $55^{0}$ so với phương nằm ngang (như hình vẽ bên dưới). Biết khoảng cách từ mắt của anh Bình đến mặt đất bằng 1,7m Chiều cao BC của đài kiểm soát không lưu bằng (làm tròn đến chữ số thập phân thứ hai)

A. $40,96 m$

B. 73,11m

C. $71,41 m$

D. 42,66m

Xem đáp án

Chọn đáp án D

Câu 17:

Để chuẩn bị tốt cho việc tham gia kỳ thi Tuyển sinh vào lớp 10 THPT, bạn An đến cửa hang sách mua thêm 1 bút bị để làm bài tự luận và 1 bút chì để làm bài trắc nghiệm khách quan. Bạn An trả cho cửa hàng hết 30 000 đồng khi mua hai cây bút trên. Mặt khác, người bán hàng cho biết tổng số tiền thu được khi bán 5 bút bi và 3 bút chì bằng với tổng số tiền thu được khi bán 2 bút bi và 5 bút chì. Giá bán của mỗi bút bi và mỗi bút chì lần lượt là

A. 14 000 đồng và 16 000 đồng

B.18 000 đồng và 12 000 đồng

C. 16 000 đồng và 14 000 đồng

D.12 000 đồng và 18 000 đồng

Xem đáp án

Chọn đáp án B

Câu 18:

Khi thả chìm hoàn toàn tượng một con ngựa nhỏ bằng đá vào một ly nước có dạng hình trụ thì người ta thấy nước trong ly dân lên thêm 1,5cm và không tràn ra ngoài. Biết diện tích đáy của ly nước bằng $80 c m^{2} .$ Thể tích của tượng đá bằng:

A. $1200 c m^{3}$

B. $120 c m^{3}$

C. $400 c m^{3}$

D. $40 c m^{3}$

Xem đáp án

Chọn đáp án A

Câu 19:

Cho đường thẳng $(d_{1}) : y = a x + b$ song song với đường thẳng $(d_{2}) : y = - 2 x + 1$ và cắt trục tung tại diểm $A (0; 3)$ . Giá trị của biểu thức $a^{2} + b^{2}$ bằng:

A. 23

B. 1

C. 81

D. 13

Xem đáp án

Chọn đáp án C

Câu 20:

Cho điểm $A (a; b)$ là giao điểm của hai đường thẳng (d) và (l) như hình vẽ bên dưới

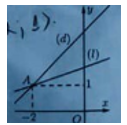
Cặp số (a,b) là nghiệm của hệ phương trình nào sau đây ?

A. $\{\begin{cases} 5 x - 4 y = - 14 \\ 4 x + 5 y = - 3 \end{cases}$

B. $\{\begin{cases} 2 x - 3 y = 8 \\ 3 x + 2 y = - 1 \end{cases}$

C. $\{\begin{cases} 2 x - 5 y = - 9 \\ 3 x - 6 y = 0 \end{cases}$

D. $\{\begin{cases} 3 x + 4 y = 5 \\ 4 x + 3 y = 2 \end{cases}$

Xem đáp án

Chọn đáp án A

Câu 21:

Vẽ đồ thị của hàm số

y = - 2 x^{2}

Xem đáp án

Học sinh tự vẽ Parabol

Câu 22:

Giải các phương trình và hệ phương trình sau:

$a) x^{2} - x - 20 = 0$

Xem đáp án

a, $x^{2} - x - 20 = 0$

$\begin{array}{l} \Leftrightarrow x^{2} - 5 x + 4 x - 20 = 0 \\ \Leftrightarrow x (x - 5) + 4 (x - 5) = 0 \\ \Leftrightarrow (x + 4) (x - 5) = 0 \\ \Leftrightarrow [\begin{array}{l} x + 4 = 0 \\ x - 5 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 4 \\ x = 5 \end{array} \end{array}$

Vậy tập nghiệm của phương trình $S = \{- 4; 5\}$

Câu 23:

Giải các phương trình và hệ phương trình sau:

$b) 4 x^{4} - 5 x^{2} - 9 = 0$

Xem đáp án

b, $4 x^{4} - 5 x^{2} - 9 = 0$

Đặt $x^{2} = t (t \geq 0) .$ Khi đó phương trình trở thành: $4 t^{2} - 5 t - 9 = 0 (*)$

Phương trình có dạng $a - b + c = 0$ nên có hai nghiệm phân biệt

$[\begin{array}{l} t_{1} = - 1 (k t m) \\ t = \frac{9}{4} \end{array} \Leftrightarrow [\begin{array}{l} x \in \emptyset \\ [\begin{array}{l} x = \frac{3}{2} \\ x = - \frac{3}{2} \end{array} \end{array}$

Vậy tập nghiệm của phương trình là $S = \{- \frac{3}{2}; \frac{3}{2}\}$

Câu 24:

Giải các phương trình và hệ phương trình sau: $c) \{\begin{cases} 2 x - y = 8 \\ 3 x + 5 y = - 1 \end{cases}$

Xem đáp án

c, $\{\begin{cases} 2 x - y = 8 \\ 3 x + 5 y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} 10 x - 5 y = 40 \\ 3 x + 5 y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} 13 x = 39 \\ y = 2 x - 8 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = - 2 \end{cases}$

Vậy nghiệm của hệ là $(x; y) = (3; - 2)$

Câu 25:

a, Trong mặt phẳng tọa độ Oxy cho parabol $(P) : y = x^{2}$ và đường thẳng $(d) : y = 2 x + 4 m^{2} - 8 m + 3$ (m là tham số thực). Tìm các giá trị của m để (d) và (P)cắt nhau tại hai điểm phân biệt $A (x_{1}; y_{1}), B (x_{2}; y_{2})$ thỏa mãn điều kiện $y_{1} + y_{2} = 10$

Xem đáp án

a) Phương trình hoành độ giao điểm của (P) và (d) là:

$x^{2} - 2 x - 4 m^{2} + 8 m - 3 = 0 (1)$

Số giao điểm của (d) và (P) cũng chính là số nghiệm của phương trình (1)

Để (d) cắt (P) tại hai điểm phân biệt $A (x_{1}; y_{1}), B (x_{2}; y_{2})$ khi và chỉ khi phương trình (1) có hai nghiệm phân biệt $x_{1}; x_{2}$

Ta có: $Δ' = {(- 1)}^{2} + 4 m^{2} - 8 m + 3 = 4 m^{2} - 8 m + 4 = 4 {(m - 1)}^{2}$

Phương trình (1) có hai nghiệm phân biệt $x_{1}, x_{2}$ khi và chỉ khi $Δ' > 0 \Leftrightarrow 4 {(m - 1)}^{2} > 0 \Leftrightarrow m \neq 1$

Áp dụng hệ thức Vi et ta có: $\{\begin{cases} x_{1} + x_{2} = 2 \\ x_{1} x_{2} = - 4 m^{2} + 8 m - 3 \end{cases}$

Theo đề bài ta có:

$\begin{array}{l} y_{1} + y_{2} = 10 \Leftrightarrow x_{1}^{2} + x_{2}^{2} = 10 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} = 10 \\ \Leftrightarrow 2^{2} - 2. (- 4 m^{2} + 8 m - 3) = 10 \Leftrightarrow 4 + 8 m^{2} - 16 m + 6 = 10 \\ \Leftrightarrow 8 m^{2} - 16 m = 0 \Leftrightarrow 8 m (m - 2) = 0 \Leftrightarrow [\begin{array}{l} m = 0 (t m) \\ m = 2 (t m) \end{array} \end{array}$

Vậy với $m = 0, m = 2$ thỏa mãn yêu cầu bài toán

Câu 26:

b ,Trong kỳ thi Tuyển sinh lớp 10 THPT năm 2019, tổng chỉ tiêu tuyển sinh của trường THPT A và trường THPT B là 900 học sinh. Do cả hai trường đều có chất lượng giáo dục rất tốt nên sau khi hết thời gian điều chỉnh nguyện vọng thì số lượng thí sinh đăng ký dự tuyển vào trường THPT A và trường THPT B tăng lần lượt là $15 %$ và $10 %$ so với chỉ tiêu ban đầu. Vì vậy, tổng số thí sinh đăng ký dự tuyển của hai trường là 1010Hỏi số lượng thí sinh đăng ký dự tuyển của mỗi trường là bao nhiêu ?

Xem đáp án

b,

a) Gọi số lượng thí sinh đăng ký dự tuyển theo chỉ tiêu của trường THPT A là x (học sinh) $(x \in ℕ *, x < 900)$

Số lượng thí sinh đăng ký dự tuyển theo chỉ tiêu của trường THPT B là y(học sinh), $(y \in ℕ *, y < 900)$

Do tổng chỉ tiêu tuyển sinh của trường THPT A và THPT B là 900 học sinh nên ta có phương trình: $x + y = 900 (1)$

Sau khi hết thời gian điều chỉnh nguyện vọng thì số lượng thí sinh đăng ký dự tuyển vào trường THPT A là : $115 % x$ (học sinh)

Sau khi hết thời gian điều chỉnh nguyện vọng thì số lượng thí sinh đăng ký dự tuyển vào trường THPT B là: $110 % x$ (học sinh)

Khi đó tổng số thí sinh đăng ký cả 2 trường là 1010 học sinh nên ta có phương trình là: $115 % x + 110 % y = 1010 \Leftrightarrow 1,15 x + 1,1 y = 1010 (2)$

Từ (1) và (2) ta có hệ phương trình:

$\{\begin{cases} x + y = 900 \\ 1,15 x + 1,1 y = 1010 \end{cases} \Leftrightarrow \{\begin{cases} x = 400 (t m) \\ y = 500 (t m) \end{cases}$

Vậy số lượng học sinh đăng ký dự tuyến vào

THPT A: $115 % .400 = 460$ (học sinh)

THPT B: $1010 - 460 = 550$ (học sinh)

Câu 27:

Cho tam giác ABC (AB > AC) nội tiếp đường tròn tâm O. Các đường cao BD và CE cắt nhau tại H $(D \in A C, E \in A B) .$ Gọi M,N lần lượt là trung điểm của các cạnh AB và AC

Chứng minh các tứ giác $B C D E, A M O N$ nội tiếp

Xem đáp án

Cho tam giác ABC (AB > AC) nội tiếp đường tròn tâm O. Các đường cao BD và CE cắt nhau tại H (ảnh 1)

tứ giác BCDE có $\hat{B E C} = \hat{B D C} = 90^{0} (g t) \Rightarrow$ Tứ giác BCDE là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau)

Ta có: M là trung điểm AB (gt) $\Rightarrow O M ⊥ A B \Rightarrow \hat{O A M} = 90^{0}$ (tính chất đường kính dây cung).

Tương tự N là trung điểm của $A C (g t) \Rightarrow O N ⊥ A C \Rightarrow \hat{O N A} = 90^{0}$ (tính chất đường kính dây cung)

Xét tứ giác AMON có $\hat{O M A} + \hat{O N A} = 90^{0} + 90^{0} = 180^{0} \Rightarrow$ Tứ giác AMON là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng $180^{0})$

Câu 28:

b, Chứng minh $A E . A M = A D . A N$

Xem đáp án

b, Tứ giác BCDE nội tiếp (cmt) $\Rightarrow \hat{A E D} = \hat{A C B}$ (góc ngoài bằng góc trong tại đỉnh đối diện )

Dễ thấy MN là đường trung bình của tam giác $A B C \Rightarrow M N / / B C$

$\Rightarrow \hat{A C B} = \hat{A N M}$ (đồng vị) $\Rightarrow \hat{A E D} = \hat{A N M} (= \hat{A C B})$

Dễ thấy MN là đường trung bình của tam giác $A B C \Rightarrow M N / / B C$

$\Rightarrow \hat{A C B} = \hat{A N M}$ (đồng vị ) $\Rightarrow \hat{A E D} = \hat{A N M} (= \hat{A C B})$

Xét $Δ A E D$ và $Δ A N M$ có:

$\hat{E A N}$ chung; $\hat{A E D} = \hat{A N M} (c m t)$

$\Rightarrow Δ A E D ~ Δ A N M (g . g) \Rightarrow \frac{A E}{A N} = \frac{A D}{A M} \Rightarrow A E . A M = A D . A E$

Câu 29:

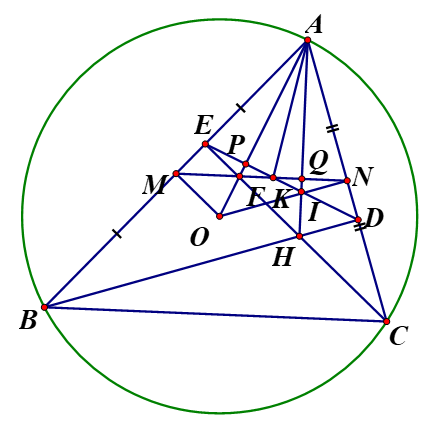
c, Gọi K là giao điểm của ED và MN, F là giao điểm của AO và MN, I là giao điểm của ED và AH Chứng minh F là trực tâm của tam giác KAI

Xem đáp án

Gọi $P = O A \cap E D; Q = M N \cap A H$

$H = B D \cap C E \Rightarrow H$ là trực tâm của tam giác $A B C \Rightarrow A H ⊥ B C$

Ta có $M N / / B C (c m t); A H ⊥ B C (c m t) \Rightarrow M N ⊥ A H$ tại Q

Xét $Δ A M Q$ và $Δ A O N$ có:

$\hat{A M Q} = \hat{A M N}$ (hai góc nội tiếp cùng chắn cung AN)

$\hat{A Q M} = \hat{A N O} = 90^{0}$

$\Rightarrow Δ A M Q ~ Δ A O N (g . g) \Rightarrow \hat{M A Q} = \hat{O A N}$ (hai góc tương ứng)

$\begin{array}{l} \Rightarrow \hat{M A Q} - \hat{Q A O} = \hat{O A N} - \hat{Q A O} \\ \Rightarrow \hat{O A M} = \hat{Q A N} \Rightarrow \hat{P A E} = \hat{Q A N} \end{array}$

Lại có: $\hat{A E D} = \hat{A N M} (c m t) \Rightarrow \hat{A E P} = \hat{A N Q} \Rightarrow \hat{P A E} + \hat{A E P} = \hat{Q A N} + \hat{A N Q}$

Xét tam giác vuông AQN có: $\hat{Q A N} + \hat{A N Q} = 90^{0} \Rightarrow \hat{P A E} + \hat{A E P} = 90^{0}$

$\Rightarrow Δ A P E$ vuông tại P $\Rightarrow A P ⊥ P E$ hay $F A ⊥ K I (1)$

Ta đã chứng minh $M N ⊥ A H \Rightarrow F Q ⊥ A I (2)$

Từ (1) và (2) $\Rightarrow F$ là giao điểm của 2 đường cao $F A, F Q$ của tam giác KAI

Vậy F là trực tâm tam giác $K A I (d f c m)$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 14

Danh sách câu hỏi

Bài thi liên quan