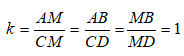Bài tập: Các trường hợp đồng dạng của tam giác (có lời giải chi tiết)
-
941 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hai tam giác Δ RSK và Δ PQM có: RS/PQ = RK/PM = SK/QM thì:
Ta có: RS/PQ = RK/PM = SK/QM ⇒ Δ RSK đồng dạng Δ PQM
Chọn đáp án A.
Câu 2:
Nếu Δ RSK đồng dạng Δ PQM có: RS/PQ = RK/PM = SK/QM thì
Ta có Δ RSK đồng dạng Δ PQM ⇔
Chọn đáp án A.
Câu 3:
Cho tam giác ABC có M và N lần lượt là trung điểm của AC và AB. Gọi AD là tia phân giác của , tia AD cắt MN tại P. Hỏi tam giác nào đồng dạng với tam giác ANP?
Xét tam giác ABC có M và N lần lượt là trung điểm của AC và AB nên MN là đường trung bình của tam giác ABC
Suy ra: MN // BC
Xét tam giác ABD có MP// BD (vì MN// BC)
Suy ra: Tam giác ANP đồng dạng với tam giác ABD.
Chọn đáp án A
Câu 5:
Cho tam giác ABC có M là trung điểm của AC. Lấy điểm D đối xứng với B qua M . Khi đó:
Xét Δ AMB và ΔCMD có:
AM = MC ( vì M là trung điểm của AC)
∠AMB = ∠CMD = 90o
BM = MD ( vì D đối xứng với B qua M)
Suy ra: Δ AMB = ΔCMD ( c.g.c)
Suy ra: Hai tam giác này cũng đồng dạng với nhau và tỉ số đồng dạng là:
Chọn đáp án C
Câu 6:
Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên suy ra ΔABC ~ ΔDEF (c - c - c) theo tỉ số đồng dạng k = 2.
Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ đồng dạng ΔDEF theo tỉ số
Theo tính chất đường trung bình mà (cmt) suy ra
Tương tự
Do đó ΔA’B’C’ đồng dạng ΔABC theo tỉ số
Đáp án: C
Câu 7:
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. ΔABD đồng dạng với tam giác nào dưới đây?
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có:
=> ΔAEG đồng dạng ΔABD (c - c - c) (đpcm)
Đáp án: A
Câu 8:
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Chọn khẳng định đúng?
Từ câu trước ta có: => AE.AD = AB.AG (1)
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2)
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án: B
Câu 9:
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Xét các cặp tam giác sau đây, số cặp tam giác đồng dạng với nhau là:
(1) ΔAEG và ΔABD
(2) ΔADF và ΔACE
(3) ΔABC và ΔAEC
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có:
=> ΔAEG ~ ΔABD (c - c - c) nên (1) đúng.
Tương tự ta cũng chứng minh được ΔADF ~ ΔACE nên (2) đúng
Dễ thấy (3) sai vì
Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.
Đáp án: C
Câu 10:
Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. Chọn khẳng định không đúng?
Từ câu trước ta có: => AE.AD = AB.AG (1) nên A đúng
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2) nên B đúng
Ngoài ra => AD.EC = AC.FD nên C đúng
Chỉ có đáp án D sai vì
Đáp án: D
Câu 11:
Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.
Tam giác thứ nhất có các cạnh là 8 < x < y
Tam giác thứ hai có các cạnh là x < y < 27
Vì hai tam giác đồng dạng nên ta có x.y = 8.27 và .
Do đónên
Vậy x = 12, y = 18
Đáp án: C
Câu 12:
Một tam giác có cạnh nhỏ nhất bằng 12, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 40,5, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng, từ đó suy ra giá trị của S = x + y bằng:
Tam giác thứ nhất có các cạnh là 12 < x < y
Tam giác thứ hai có các cạnh là x < y < 40,5
Vì hai tam giác đồng dạng nên ta có x.y = 12.40,5 và .
Do đó nên suy ra x = 18
Suy ra
Vậy x = 18, y = 27 => S = 18 + 27 = 45
Đáp án: A