Bài tập Toán 8 Chủ đề 13: Luyện tập đường thẳng song song với một đường thẳng cho trước có đáp án
Dạng 1. Luyện tập đường thẳng song song với một đường thẳng cho trước có đáp án
-
208 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho góc vuông xOy và điểm A thuộc tia Ox sao cho OA = 4cm. lấy điểm B tùy ý trên tia Oy và gọi M là trung điểm của AB . Khi B di chuyển trên tia Oy thì M di chuyển trên đường nào
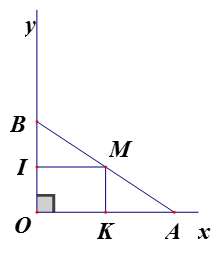
+ Kẻ
+ Tứ giác IMKO có
+ Tứ giác IMKO là hình chữ nhật
Suy ra IM = OK; MK // OI
+ Xét có M là trung điểm AB, MK // OB suy ra
+ Suy ra MI = 2cm
+ Suy ra khi B di chuyển trên tia Oy thì M di chuyển trên đường thẳng vuông góc với tia Ox tại K song song với Oy và cách Oy một khoảng 2cm
Giới hạn: Khi B trùng O thì M trùng K
khi B di chuyển trên tia Oy thì M di chuyển trên đường thẳng vuông góc với tia Ox tại K song song với Oy và cách Oy một khoảng 2cm
Vậy khi B di chuyển trên tia Oy thì M di chuyển trên tia Kt vuông góc với tia Ox tại K và cách Oy
một khoảng 2cm
Câu 2:
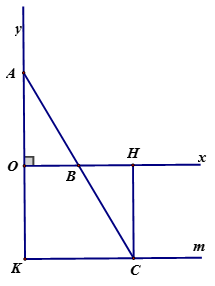
+ Vì điểm C đối xứng với AC qua B nên BA = BC
+ Kẻ
+ Xét tam giác vuông AOB và CHB có
+ Có ( đối đỉnh)
+ Do đó nên CH = AO
MÀ OA không đổi nên CH không đổi
+ Suy ra C chuyển động trên đường thẳng song song với Ox cách Ox một khoảng bằng
Khi B trùng O thì C trùng K đối xứng với A qua O
Vậy C chuyển động trên tia Km // Ox cách Ox một khoảng không đổi bằng oa
Câu 3:
Cho điểm A nằm ngoài đường thẳng d . Điểm M di chuyển trên đường thẳng d . Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào?
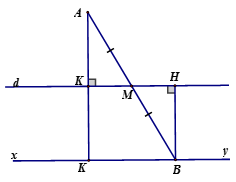
+ Kẻ
+ Có AM = MB
+ Chứng minh
+ Suy ra AK = BH
+ Điểm A cố định, đường thẳng d cố định nên AK không thay đổi
Vậy B chuyển động trên đường thẳng xy song song với d cách d một khoảng bằng AKCâu 4:
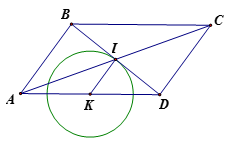
+ Gọi K là trung điểm AD. Ta có AD cố định nên K cố định
+ Trong ta có
IB = ID ( tính chất hình bình hành)
KA = KD ( theo cách vẽ)
Nên KI là đường trung bình của
Suy ra KI = AB : 2 = 2 : 2 = 1 (tính chất đường trung bình)
+ B , C thay đổi thì I thay đổi luôn cách K cố định một khoảng không đổi nên I chuyển động trên đường tròn (K,1cm)
Vậy B chuyển động trên đường thẳng xy song song với d cách d một khoảng bằng AKCâu 5:
Cho tam giác ABC cân tại A, các điểm M, N theo thứ tự di động trên các cạnh AB, AC sao cho AM = CN. Hãy tìm tập hợp trung điểm I của MN
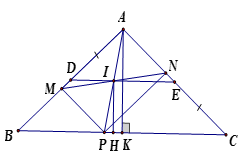
+ Kẻ NP // AB ta có ( 2 góc đồng vị); mà (GT)
Suy ra hay NPC cân
Suy ra NP = NC mà NC = MA nên NP = MA
Mà NP // MA nên tứ giác AMPN là hình bình hành có I là trung điểm MN
Suy ra I là trung điểm AP
+ Kẻ IH và AK cùng vuông góc với BC ta có IH là đường trung bình của APK nên (không đổi)
Vậy tập hợp các trung điểm I của MN khi M, N di động trên AB, AC là đường trung bình của ABC và DE // BC trong đó D là trung điểm cạnh AB, E là trung điểm cạnh ACCâu 6:
Qua A dựng đường thẳng d song song vói CC’
Ta có : và
Theo định lí về đường thẳng song song cách đều ta suy ra các đường thẳng d là các đường thẳng song song cách đều nên nó chắn trên AB các đoạn thẳng liên tiếp bằng nhau
Hay
Vậy đoạn thẳng AB bị chia ra ba phần bằng nhau.
Câu 7:
Cho ABC có D là trung điểm của AB, kẻ DE // BC . Chứng minh rằng AE = EC.
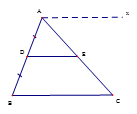
Do DE // BC (GT) nên vẽ thêm Ax // DE thì Ax // DE // BC (1)
Vì D là trung điểm của AB nên AD = DB
Từ (1) và (2) suy ra Ax, DE, BC là ba đường thẳng song song cách đều nên nó chắn trên đường thẳng AC hai đoạn thẳng liên tiếp bằng nhau là AE = EC.
Câu 8:
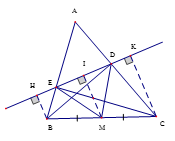
Vì BD, CE là các đường cao của ABC nên , do đó BDC vuông tại D, CEB vuông tại E.
Gọi M là trung điểm của BC, vẽ DM, EM thì DM, EM là các trung tuyến ứng với cạnh huyền của BDC và CEB.
Áp dụng tính chất đường trung tuyến ứng với cạnh huyền vào 2 tam giác vuông trên, ta được:
cân tại M
Từ giả thiết ta có tứ giác BKHC là hình thang vuông nên vẽ thêm thì BH // MI // CK (1)
Mà BM = MC (cách vẽ) (2)
Từ (1) và (2) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK (3)
Ta có DM = EM suy ra MDE cân tại M , có MI là đường cao ứng vói cạnh đáy DE nên EI = ID (4)
Trừ theo vế đẳng thức (3) cho (4) ta được EH = DKCâu 9:
Cho điểm A ở ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Trên d lấy một điểm B bất kì. Gọi C là điểm đối xứng với điểm A qua điểm B . Hỏi khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?
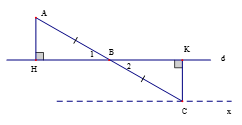
Kẻ và thì AH là khoảng cách từ điểm A cố định đến đường thẳng d cố định nên AH = 2cm không đổi, CK là khoảng cách từ C đến đường thẳng d. Khi B di chuyển trên d thì điểm C cũng di chuyển theo.
Áp dụng tính chất của điểm đối xứng qua tâm và góc đối đỉnh ta được :
nên
Như vậy điểm C cách đường thẳng d cố định một khoảng không đổi 2cm. nên C di chuyển trên đường thẳng Cx // d và cách d một khoảng bằng 2cm.Câu 10:
Cho hình thang vuông có DC = 2AB = BC. Tính số đo .
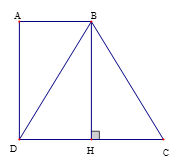
Vẽ hình xong ta dự đoán rằng BDC đều. Để chứng minh BDC đều ta chỉ cần chứng minh BDC cân đỉnh B là đủ.
Suy ra ta cần vẽ thêm đường phụ ,
Vẽ
Ta có nên AD // DH.
Mặt khác AB // DC, AD // BH nên AB = DH ( tính chất đoạn chắn)
Mà DC = 2AB (GT) và AB = DH => DC = 2DH
Suy ra H là trung điểm của DC.
BDC có BH là đường cao và là trung tuyến nên BDC cân tại B
Suy ra đều
Mà (vì AB // DC ) do đó :
