Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Đường trung bình của tam giác, của hình thang có đáp án
Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Đường trung bình của tam giác, của hình thang có đáp án
-
280 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho Δ ABC có M là trung điểm của AB, N là trung điểm của AC và BC = 4( cm ). Tính độ dài MN.
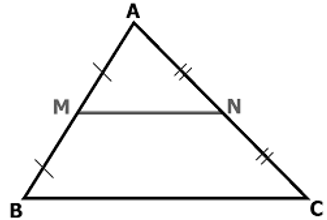
Theo giả thiết ta có M là trung điểm của AB, N là trung điểm của AC
⇒ MN là đường trung bình của Δ ABC.
Áp dụng định lý 2, ta có MN = BC.
⇒ MN = BC = .4 = 2( cm )
Câu 2:
Cho hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC và AB = 4( cm ) và CD = 7( cm ). Tính độ dài đoạn EF.
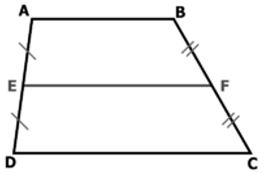
Ta có hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC
⇒ EF là đường trung bình của hình thang.
Áp dụng định lý 2, ta có EF =
⇒ EF = = 5,5( cm ).
Câu 3:
Cho tam giác ABC( AB > AC ) có = 500. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E,F lần lượt là trung điểm của cạnh AD, BC. Tính = ?
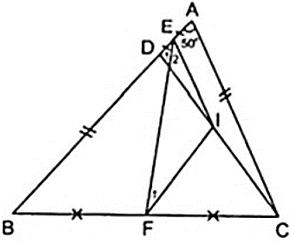
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác BCD và ACD.
Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
( 1 ) FI//BD ( 2 ) FI = a
( 3 ) EI = a ( 4 ) EI//AC
Từ ( 1 ) ⇒ (vì so le trong) ( 5 )
Từ ( 2 ) và ( 3 ) ⇒ FI = EI nên (vì trong tam giác, đối diện với hai cạnh bằng nhau là hai góc bằng nhau) ( 6 )
Từ ( 5 ) và ( 6 ) ⇒
Từ ( 4 ) ⇒ = 500 (vì đồng vị)
Mà = 250
Câu 4:
Cho hình thang ABCD ( AB//CD ) có AB = 2cm, CD = 5cm, AD = 7cm. Gọi E là trung điểm của BC. Tính = ?
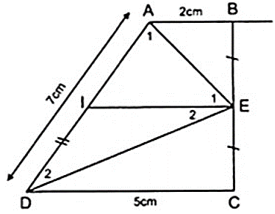
Đặt = α , = β ⇒ = α + β
Do E là trung điểm của BC theo giả thiết vẽ I là trung điểm của AD thì AI = ID = = 3,5( cm ). (1 )
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có
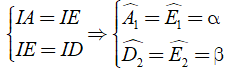
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có = 1800
Hay α + α + β + β = 2( α + β ) = 1800 ⇒ α + β = 900
Do α + β = 900 nên = 900.
Câu 5:
Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC
⇒ DE là đương trung bình của tam giác ABC
Hay DE//BC và DE = BC.
+ Hình thang cân là hình thang có hai góc kề một cạnh bằng nhau và hai cạnh bên bằng nhau nhưng bài toán này hai góc kề một cạnh đấy không bằng nhau
→ Đáp án C sai.
Câu 6:
Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC
⇒ DE là đương trung bình của tam giác ABC
Hay DE//BC và DE = BC ⇒ BC = 2DE = 2.4 = 8( cm )
Khi đó ta có: S = AH.BC = .6.8 = 24( cm2 )
Câu 7:
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
→ Đáp án A đúng.
+ Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng của hai đáy.
+ Một hình thang thì chỉ có 1 đường trung bình duy nhất.
Câu 8:
Diện tích hình thang bằng nửa tổng độ dài hai đáy nhân với đường cao của hình thang,
⇒ S = ( a + b )h
