Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Phương trình tích có đáp án
-
1354 lượt thi
-
10 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Giải phương trình ( x + 1 )( x + 4 ) = ( 2 - x )( 2 + x )
Ta có: ( x + 1 )( x + 4 ) = ( 2 - x )( 2 + x ) ⇔ x2 + 5x + 4 = 4 - x2
⇔ 2x2 + 5x = 0 ⇔ x( 2x + 5 ) = 0
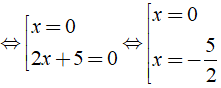
Vậy phương trình đã cho có tập nghiệm là S = { ; 0 }
Câu 2:
Giải phương trình x3 - x2 = 1 - x
Ta có: x3 - x2 = 1 - x ⇔ x2( x - 1 ) = - ( x - 1 )
⇔ x2( x - 1 ) + ( x - 1 ) = 0 ⇔ ( x - 1 )( x2 + 1 ) = 0
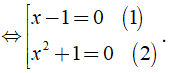
( 1 ) ⇔ x - 1 = 0 ⇔ x = 1.
( 2 ) ⇔ x2 + 1 = 0 (Vô nghiệm vì x2 ≥ 0 ⇒ x2 + 1 ≥ 1 )
Vậy phương trình đã cho có tập nghiệm là S = { 1 }.
Câu 3:
Giải các phương trình sau:
a) ( 5x - 4 )( 4x + 6 ) = 0
a) Ta có: ( 5x - 4 )( 4x + 6 ) = 0
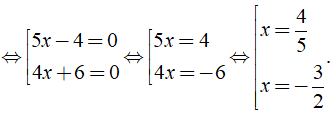
Vậy phương trình đã cho có tập nghiệm là S = { }.
Câu 4:
b) ( x - 5 )( 3 - 2x )( 3x + 4 ) = 0
b) Ta có: ( x - 5 )( 3 - 2x )( 3x + 4 ) = 0
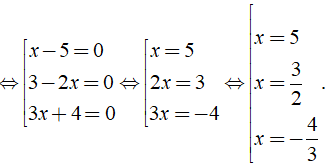
Vậy phương trình đã cho có tập nghiệm là S = { }.
Câu 5:
c) ( 2x + 1 )( x2 + 2 ) = 0
Ta có: ( 2x + 1 )( x2 + 2 ) = 0
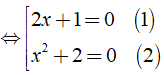
Giải ( 1 ) ⇔ 2x + 1 = 0 ⇔ 2x = - 1 ⇔ x = - 1/2.
Ta có: x2 ≥ 0 ⇒ x2 + 2 ≥ 2 ∀ x ∈ R
⇒ Phương trình ( 2 ) vô nghiệm.
Vậy phương trình đã cho có tập nghiệm S = {}.
Câu 6:
d) ( x - 2 )( 3x + 5 ) = ( 2x - 4 )( x + 1 )
d) Ta có: ( x - 2 )( 3x + 5 ) = ( 2x - 4 )( x + 1 )
⇔ ( x - 2 )( 3x + 5 ) - 2( x - 2 )( x + 1 ) = 0
⇔ ( x - 2 )[ ( 3x + 5 ) - 2( x + 1 ) ] = 0
⇔ ( x - 2 )( x + 3 ) = 0
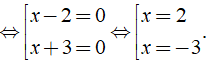
Vậy phương trình đã cho có tập nghiệm là S = { - 3;2 }.
Câu 7:
Giải các phương trình sau:
a) ( 2x + 7 )2 = 9( x + 2 )2
a) Ta có: ( 2x + 7 )2 = 9( x + 2 )2
⇔ ( 2x + 7 )2 - 9( x + 2 )2 = 0
⇔ [ ( 2x + 7 ) + 3( x + 2 ) ][ ( 2x + 7 ) - 3( x + 2 ) ] = 0
⇔ ( 5x + 13 )( 1 - x ) = 0
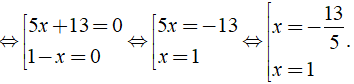
Vậy phương trình đã cho có tập nghiệm là S = { }.
Câu 8:
b) ( x2 - 1 )( x + 2 )( x - 3 ) = ( x - 1 )( x2 - 4 )( x + 5 )
b) Ta có: ( x2 - 1 )( x + 2 )( x - 3 ) = ( x - 1 )( x2 - 4 )( x + 5 )
⇔ ( x2 - 1 )( x + 2 )( x - 3 ) - ( x - 1 )( x2 - 4 )( x + 5 ) = 0
⇔ ( x - 1 )( x + 1 )( x + 2 )( x - 3 ) - ( x - 1 )( x - 2 )( x + 2 )( x + 5 ) = 0
⇔ ( x - 1 )( x + 2 )[ ( x + 1 )( x - 3 ) - ( x - 2 )( x + 5 ) ] = 0
⇔ ( x - 1 )( x + 2 )[ ( x2 - 2x - 3 ) - ( x2 + 3x - 10 ) ] = 0
⇔ ( x - 1 )( x + 2 )( 7 - 5x ) = 0
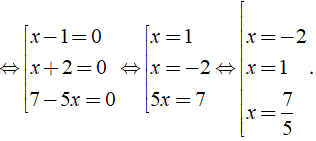
Vậy phương trình có tập nghiệm là S = { - 2; 1; }.
Câu 9:
c) ( 5x2 - 2x + 10 )2 = ( 3x2 + 10x - 8 )2
Ta có: ( 5x2 - 2x + 10 )2 = ( 3x2 + 10x - 8 )2
⇔ ( 5x2 - 2x + 10 )2 - ( 3x2 + 10x - 8 )2 = 0
⇔ [ ( 5x2 - 2x + 10 ) - ( 3x2 + 10x - 8 ) ][ ( 5x2 - 2x + 10 ) + ( 3x2 + 10x - 8 ) ] = 0
⇔ ( 2x2 - 12x + 18 )( 8x2 + 8x + 2 ) = 0
⇔ 4( x2 - 6x + 9 )( 4x2 + 4x + 1 ) = 0
⇔ 4( x - 3 )2( 2x + 1 )2 = 0
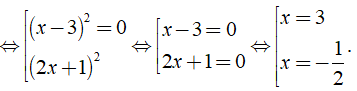
Vậy phương trình đã cho có tập nghiệm S = { ; 3 }.
Câu 10:
d) ( x2 + x )2 + 4( x2 + x ) - 12 = 0
Ta có: ( x2 + x )2 + 4( x2 + x ) - 12 = 0
Đặt t = x2 + x, khi đó phương trình trở thành:
t2 + 4t - 12 = 0 ⇔ ( t + 6 )( t - 2 ) = 0
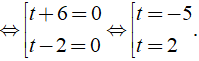
+ Với t = - 6, ta có: x2 + x = - 6 ⇔ x2 + x + 6 = 0 ⇔ ( x + 1/2 )2 + 23/4 = 0
Mà ( x + 1/2 )2 + 23/4 ≥ 23/4 ∀ x ∈ R ⇒ Phương trình đó vô nghiệm.
+ Với t = 2, ta có x2 + x = 2 ⇔ x2 + x - 2 = 0
⇔ ( x + 2 )( x - 1 ) = 0
⇔ 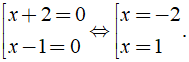
Vậy phương trình có tập nghiệm là S = { - 2;1 }.
