Chủ đề 1: Nhân đa, đơn thức có đáp án
-
368 lượt thi
-
107 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 10:
Ta có:
Tại x = 2; y = -1 thay vào ta được
Câu 29:
Ta có:
Vậy giá trị của biếu thức A không phụ thuộc vào biến x
Câu 30:
Ta có:
Vậy giá trị của biểu thức B không phụ thuộc vào biến x
Câu 31:
Ta có:
Vậy giá trị của biểu thức C không phụ thuộc vào biến x
Câu 36:
Chứng minh rằng:
với mọi số thực x, y, z
Ta có:
với mọi số thực x, y, z
Dấu “=” xảy ra khi và chỉ khi .
Câu 37:
Chứng minh rằng với thì giá trị của biểu thức:
là bình phương của một số hữu tỉ.
Ta có:
Đặt , khi đó ta có:
Vậy (đpcm)
Câu 38:
Ta có:
Vậy giá trị lớn nhất của biểu thức A là 5 khi .
Câu 39:
Ta có:
Vậy giá trị lớn nhất của biểu thức B là khi .
Câu 42:
Ta có:
Vậy giá trị nhỏ nhất của biểu thức A là 1 khi .
Câu 43:
Ta có:
Vậy giá trị nhỏ nhất của biểu thức B là khi .
Câu 44:
Tìm giá trị nhỏ nhất của biểu thức
Ta có:
Đặt thay vào ta được:
Giá trị nhỏ nhất của khi và chỉ khi
Vậy giá trị nhỏ nhất của khi và chỉ khi hoặc
Câu 45:
Ta có:
Mặt khác
Vậy giá trị nhỏ nhất của khi và chỉ khi
Câu 77:
Ta có:
Theo bài ra ta có: , thay vào A ta được:
Vậy
Câu 78:
Cho và
Tính giá trị biểu thức sau:
Theo bài ra có:
+)
(*)
+) Mặt khác theo bài ra: , thay vào phương trình (*) ta được:
(*)
+) Áp dụng hằng đẳng thức bậc 3, ta được:
Thay các giá trị phía trên vào A ta được:
Vậy .
Câu 88:
Ta có:
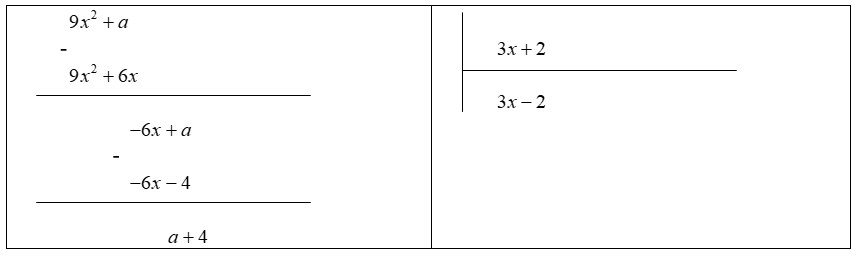
dư a + 4.
Vậy để là phép chia hết thì .
Câu 89:
chia cho có số dư bằng -2
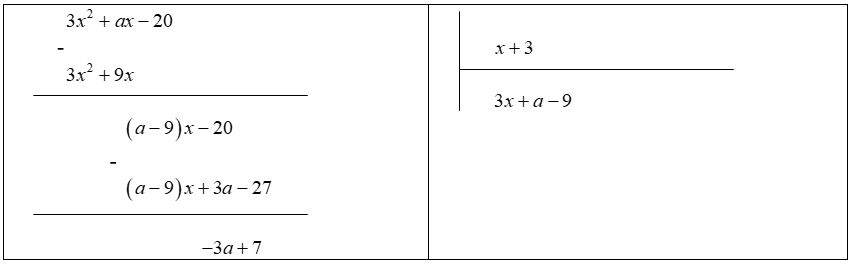
dư .
Vậy để là phép chia có số dư bằng 2 thì .
Câu 90:
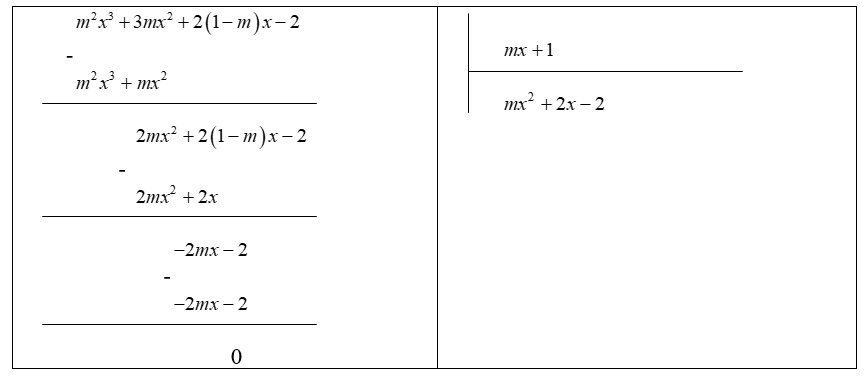
Tìm các số nguyên a và b để đa thức chia hết cho đa thức
Cách 1: Phương pháp thực hiện phép chia
Ta có:

dư .
Để là phép chia hết thì
Vậy với và thì phép chia là phép chia hết
Cách 2: Phương pháp hệ số bất định
Giả sử đa thức chia hết cho , khi đó ta được thương là nhị thức bậc hai có dạng: . Nhân thương với số chia rồi đồng nhất thức với đa thức , ta được:
Vậy với a = 12 và b = -16 thì phép chia là phép chia hết.
Câu 91:
Cách 1: Phương pháp thực hiện phép chia
Ta có:

dư .
Vậy để là phép chia hết thì .
Cách 2: Phương pháp hệ số bất định
Giả sử đa thức chia hết cho , khi đó ta được thương là nhị thức bậc hai có dạng: . Nhân thương với số chia rồi đồng nhất thức với đa thức , ta được:
Vậy với a = 30 thì đa thức chia hết cho .
Cách 3: Phương pháp trị số riêng.
Gọi thương của phép chia là khi đó ta có:
với mọi x. (1)
+) Với x = - 2, thay vào (1) ta được:
Vậy với a = 30 thì đa thức chia hết cho .
Câu 92:
Cho hai đa thức và đa thức
Thực hiện phép chia đa thức A cho đa thức B
Thực hiện phép chia ta được:
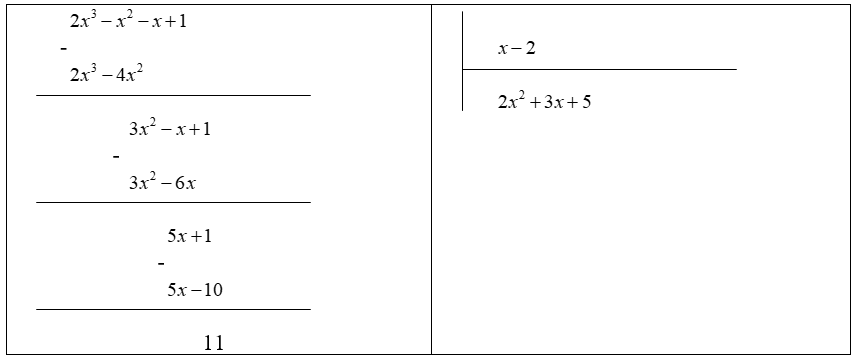
Vậy đa thức dư 11.
Câu 93:
Theo câu a ta có:
Để là phép chia hết thì 11 phải chia hết cho , tức là phải là ước của 11.
Vậy để đa thức chia hết cho thì
Câu 94:
Hiện nay tuổi mẹ 32 tuổi, tuổi con là 8 tuổi. Hỏi cách đây bao nhiêu năm tuổi mẹ gấp 5 lần tuổi con.
Gọi số năm để tuổi mẹ gấp 5 lần tuổi con là n với
Theo bài ra ta có:
Vậy cách đây 2 năm tuổi mẹ gấp 5 lần tuổi con.
Câu 95:
Tìm ba số tự nhiên lẻ liên tiếp nhau, biết số thứ nhất nhân với số thứ hai bé hơn số thứ nhất nhân với số ba là 18.
Gọi ba số tự nhiên lẻ liên tiếp nhau là , , với
Theo bài ra ta có:
.
Vậy ba số tự nhiên lẻ liên tiếp cần tìm là: 9, 11 và 13.
Câu 96:
Bể bơi tại một ngôi trường có hình chữ nhật với chiều rộng là và chiều dài là
Diện tích bể bơi trên theo x và y.
Do bể có hình chữ nhật nên diện tích của bể bơi:
.Câu 97:
Bể bơi tại một ngôi trường có hình chữ nhật với chiều rộng là và chiều dài là .
Với m và m diện tích bể bơi là:
m2
Vậy diện tích bể bơi là 105 m2.
Câu 98:
Một xe buýt xuất phát trên xe có x hành khách, đến bến thứ nhất có 3 hành khách lên xe, đến bến thứ 2 số hành khách trên xe đã tăng lên gấp đôi, đến bến thứ 3 có 1 hành khách lên xe và 5 hành khách xuống xe, đến bến thứ 4 không có hành khách lên hay xuống xe, đến bến thứ 5 có 2 hành khách lên xe sau đó tài xế đếm được trên xe có 20 hành khách. Hỏi lúc xuất phát xe buýt có bao nhiêu hành khách.
Số hành khách lúc xuất phát là hành khách .
+) Bến thứ nhất có 3 hành khách lên xe, số hành khách trên xe là: .
+) Bến thứ 2 số hành khách trên xe đã tăng lên gấp đôi, số hành khách trên xe là .
+) Bến thứ 3 có 1 hành khách lên xe và 5 hành khách xuống xe, số hành khách trên xe là: .
+) Bến thứ 4 không có hành khách lên hay xuống xe, số hành khách trên xe là .
+) Bến thứ 5 có 2 hành khách lên xe, số hành khách trên xe là:
Tại bến thứ 5 tài xế đếm được trên xe có 20 hành khách, nên ta có:
.
Vậy số hành khách lúc xuất phát là 8 hành khách.
Câu 99:
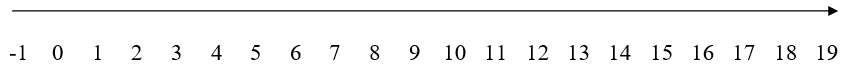
+) Trục số ở trên biểu diễn các tầng của thang máy với tầng G là gốc 0,
Tầng 1, 2, 3, … 12, 12A, 14, 15, … 19 tương ứng là các số nguyên từ 1 đến 19, Tầng hầm tương ứng với -1.
+) Chiều thàng máy đi lên là +, chiều đi xuống là -.
+) Theo bài ra cuối cùng thang máy dừng ở tầng:
Vậy cuối cùng thang máy dừng ở tầng G.
Câu 100:
Tìm hai số tự nhiên lẻ liên tiếp nhau, biết hiệu bình phương của hai số bằng 48.
Gọi hai số tự nhiên lẻ liên tiếp nhau là , với .
Theo bài ra ta có:
Vậy ba số tự nhiên lẻ liên tiếp cần tìm là: 11 và 13.
Câu 101:
Bác Năm có 40m lưới muốn vây quanh một chiếc ao hình chữ nhật để nuôi vịt. Hỏi diện tích lớn nhất của chiếc ao bằng bao nhiêu để bác Năm có thể vây kín xung quanh.
+) Ta có nửa chu vi là: (m)
Mặt khác: nửa chu vi = (dài + rộng) dài + rộng = 20 (m)
+) Gọi x là chiều rộng của chiếc ao hình chữ nhật
Chiều dài của ao là (m).
+) Diện tích của hình chữ nhật là:
Dâu “=” xảy ra khi và chỉ khi .
Với chiều dài = chiều rộng = 10
Vậy diện tích lớn nhất của chiếc ao bằng 100m2 với chiều rộng bằng chiều dài bằng 10m (ao có hình vuông)
Câu 102:
Người ta muốn rào quanh một khu đất với một số vật liệu cho trước là 80 mét. Ở đó người ta tận dụng một hàng rào đã có sẵn để làm một cạnh của hàng rào và rào thành mảnh đất hình chữ nhật. Hỏi mảnh đất hình chữ nhật được rào có diện tích lớn nhất bằng bao nhiêu?
+) Gọi x là độ dài của cạnh song song với hàng rào đã có sẵn
Và y là độ dài của cạnh vuông góc với hàng rào đã có sẵn
Theo bài ra ta có:
+) Diện tích của mảnh đất
.
Dấu “=” xảy ra khi và chỉ khi .
Với
Vậy diện tích lớn nhất của khu đất bằng 800m2 với chiều dài bằng 40m, chiều rộng bằng 20m.
Câu 103:
Tìm các số thực a, b, sao cho đa thức ![]() chia hết cho đa thức
chia hết cho đa thức ![]() .
.
(Thi học sinh giỏi lớp 9, TP Hà Nội, năm học 2012 - 2013)
Tìm cách giải. Khi tìm hệ số a, b sao cho đa thức f(x) chia hết cho đa thức g(x), chúng ta có hai hướng suy nghĩ:
Đặt phép chia f(x) cho g(x) đến khi được phần dư có bậc nhỏ hơn bậc của đa thức g(x). Để phép chia hết ta đồng nhất phần dư đó với đa thức 0.
Còn nếu đa thức g(x) phân tích được thành nhân tử với các nhân tử bậc nhất, ta viết f(x) thành tích các nhân tử đó nhân với đa thức thương. Rồi dùng đồng nhất thức sao cho vế phải bằng 0.
Trình bày lời giải
Cách 1. Thực hiện phép chia ta được:
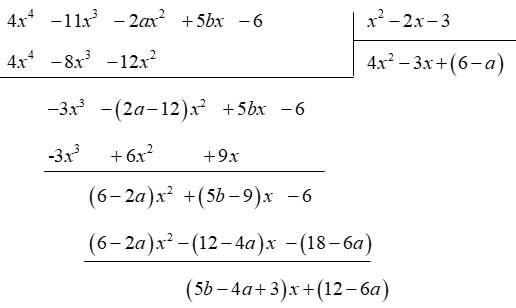
Để phép chia hết thì ![]()
Cách 2. Ta có: ![]()
![]()
Đặt thương là q(x) ta có: ![]()
Chọn x = 3 ta có: ![]()
![]() (1)
(1)
Chọn x = -1 ta có: ![]()
![]() (2)
(2)
Từ (1) và (2) suy ra: ![]()
Thay vào (2) ![]() .
.
Câu 104:
Tìm một đa thức bậc ba, biết P(x) chia cho (x - 1), (x - 2), (x - 3) đều được dư 6 và ![]() .
.
Tìm cách giải. Từ đề bài theo định lí Bézout ta có ![]() . Như vậy đa thức P(x) bậc ba mà biết giá trị tại bốn điểm 1; 2; 3; - 1 nên ta có thể sử dụng phương pháp nội suy Newton.
. Như vậy đa thức P(x) bậc ba mà biết giá trị tại bốn điểm 1; 2; 3; - 1 nên ta có thể sử dụng phương pháp nội suy Newton.
Trình bày lời giải
Theo định lý Bézout ta có: ![]() .
.
Do đó ta đặt ![]()
Cho x = 1 ta được ![]() , suy ra d = 6
, suy ra d = 6
![]()
Cho x = 2 ta được ![]() , suy ra c = 0
, suy ra c = 0
![]()
Cho x = 3 ta được ![]() , suy ra b = 0
, suy ra b = 0
![]()
Do đó ![]() .
.
Cho x = -1 ta được ![]() , do đó
, do đó ![]() suy ra a = 1.
suy ra a = 1.
Vậy ![]()
Rút gọn ta được: ![]() .
.
Câu 105:
Tìm cách giải. Đa thức g(x) bậc n có n nghiệm phân biệt. Nếu mọi nghiệm của đa thức g(x) cũng là nghiệm của đa thức f(x) thì đa thức f(x) chia hết cho đa thức g(x). Nhận thấy trong bài g(x) có hai nghiệm là x = 2; x = 3, nên chúng ta chỉ cần kiểm tra xem x= 2; x = 3 có là nghiệm của f(x) không?
Trình bày lời giải
Ta có: ![]() nên
nên ![]()
![]() nên
nên ![]()
Nên f(x) chia hết cho ![]()
Câu 106:
Tìm các giá trị nguyên của x để giá trị của đa thức ![]() chia hết cho giá trị của đa thức B = x + 3.
chia hết cho giá trị của đa thức B = x + 3.
Giải
Đặt phép chia ta có:
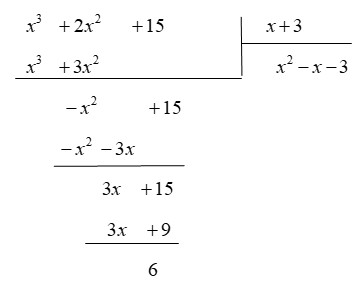
|
x + 3 |
1 |
-1 |
2 |
-2 |
3 |
-3 |
6 |
-6 |
| x |
-2 |
-4 |
-1 |
-5 |
0 |
-6 |
3 |
-9 |
Vậy với ![]() thì giá trị của biểu thức A chia hết cho giá trị của biểu thức B.
thì giá trị của biểu thức A chia hết cho giá trị của biểu thức B.
Câu 107:
Tính giá trị biểu thức ![]() khi
khi ![]()
Tìm cách giải. Với ![]() thì tìm x, ta được x không phải là số nguyên, nên thay vào biểu thức P để tính sẽ gặp nhiều khó khăn và có thể dẫn đển sai lầm. Do vậy chúng ta sử dụng P chia cho
thì tìm x, ta được x không phải là số nguyên, nên thay vào biểu thức P để tính sẽ gặp nhiều khó khăn và có thể dẫn đển sai lầm. Do vậy chúng ta sử dụng P chia cho ![]() được Q(x) và phần dư R(x) khi đó, ta viết:
được Q(x) và phần dư R(x) khi đó, ta viết: ![]() . Sau đó thay
. Sau đó thay ![]() vào biểu thức, ta tính được P(x) đơn giản hơn.
vào biểu thức, ta tính được P(x) đơn giản hơn.
Trình bày lời giải
Ta có:
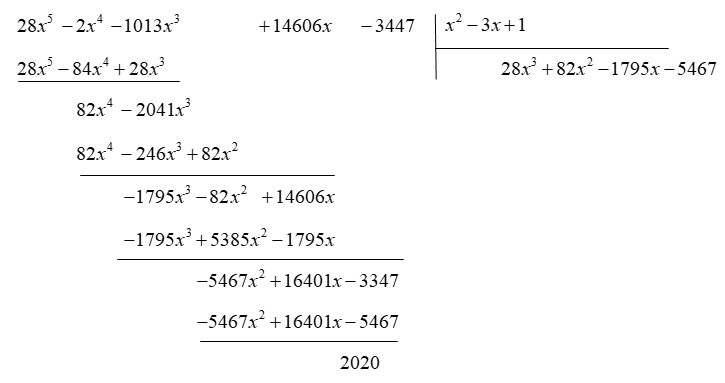
Từ đó ta có ![]() mà
mà ![]()