Trắc nghiệm Chuyên đề 8 Chủ đề 8: Ôn tập và kiểm tra (có đáp án)
-
541 lượt thi
-
62 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Ta có A = x( 2x + 3 ) - 4( x + 1 ) - 2x( x - ) = ( 2x.x + 3.x ) - ( 4.x + 4.1 ) - ( 2x.x - .2x )
= 2x2 + 3x - 4x - 4 - 2x2 + x = - 4.
Chọn đáp án C.
Câu 2:
Chọn câu trả lời đúng ( 2x3 - 3xy + 12x )( - xy ) bằng ?
Ta có: ( 2x3 - 3xy + 12x )( - xy ) = ( - xy ).2x3 - 3xy( - xy ) + 12x( - xy )
= - x4y + x2y2 - 2x2y
Chọn đáp án D.
Câu 3:
Kết quả nào sau đây đúng với biểu thức A = xy( x2y -5x + 10y ) ?
Ta có: A = xy( x2y -5x + 10y ) = xy.x2y - xy.5x + xy.10y
= x3y2 - 2x2y + 4xy2.
Chọn đáp án C.
Câu 4:
Kết quả của phép tính ( x - 2 )( x + 5 ) bằng ?
Ta có ( x - 2 )( x + 5 ) = x( x + 5 ) - 2( x + 5 )
= x2 + 5x - 2x - 10 = x2 + 3x - 10.
Chọn đáp án B.
Câu 5:
Thực hiện phép tính ( 5x - 1 )( x + 3 ) - ( x - 2 )( 5x - 4 ) ta có kết quả là ?
Ta có ( 5x - 1 )( x + 3 ) - ( x - 2 )( 5x - 4 ) = 5x( x + 3 ) - ( x + 3 ) - x( 5x - 4 ) + 2( 5x - 4 )
= 5x2 + 15x - x - 3 - 5x2 + 4x + 10x - 8 = 28x - 11
Chọn đáp án C.
Câu 6:
Điền vào chỗ trống: A = ( x - y )2 = x2 - ... + y2
Áp dụng hằng đẳng thức ( a + b )2 = a2 + 2ab + b2.
Khi đó ta có A = ( x - y )2 = x2 - 2.x.y + y2 = x2 - xy + y2.
Suy ra chỗ trống cần điền là xy.
Chọn đáp án B.
Câu 7:
Điều vào chỗ trống: ... = ( 2x - 1 )( 4x2 + 2x + 1 ).
Áp dụng hằng đẳng thức a3 - b3 = ( a - b )( a2 + ab + b2 )
Khi đó ta có ( 2x - 1 )( 4x2 + 2x + 1 ) = ( 2x - 1 )[ ( 2x )2 + 2x.1 + 1 ] = ( 2x )3 - 1 = 8x3 - 1.
Suy ra chỗ trống cần điền là 8x3 - 1.
Chọn đáp án D.
Câu 8:
Đa thức 4x( 2y - z ) + 7y( z - 2y ) được phân tích thành nhân tử là ?
Ta có 4x( 2y - z ) + 7y( z - 2y ) = 4x( 2y - z ) - 7y( 2y - z ) = ( 2y - z )( 4x - 7y ).
Chọn đáp án B.
Câu 9:
Kết quả nào sau đây đúng?
Ta có
+ ( 10xy2 ):( 2xy ) = 5y
⇒ Đáp án A sai.
+ ( - x4y5z ):( x3y2z ) = - xy3
⇒ Đáp án B sai.
+ ( - xy2 )2:( x2y3 ) = ( x2y4 ):(x2y3 ) = y
⇒ Đáp án C đúng.
+ ( - 3x2y2z ):( - yz ) = 3x2y
⇒ Đáp án D sai.
Chọn đáp án C.
Câu 10:
Ta có: ( - 3 )6:( - 2 )3 = 36:( - 23 ) = 729:( - 8 ) = - .
Chọn đáp án C.
Câu 11:
Đa thức M thỏa mãn xy2 + x2y2 + x3y = ( 5xy ). M là ?
Ta có xy2 + x2y2 + x3y = ( 5xy ).M
⇒ M = ( xy2 + x2y2 + x3y ):( 5xy )
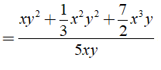
= y + xy + x2.
Chọn đáp án B.
Câu 12:
Kết quả nào sau đây đúng ?
Ta có:
+ ( - 3x3 + 5x2y - 2x2y2 ):( - 2 ) = x3 - x2y + x2y2
⇒ Đáp án A sai.
+ ( 3x3 - x2y + 5xy2 ):( x ) = 6x2 - 2xy + 10y2
⇒ Đáp án B đúng.
+ ( 2x4 - x3 + 3x2 ):( - x ) = - 6x3 + 3x2 - 9x
⇒ Đáp án C sai.
+ ( 15x2 - 12x2y2 + 6xy3 ):( 3xy ) = 5 - 4xy - 2y2
⇒ Đáp án D sai.
Chọn đáp án B.
Câu 13:
Kết quả của phép chia ( 7x3 - 7x + 42 ):( x2 - 2x + 3 ) là ?
Ta có phép chia
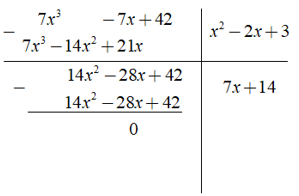
Chọn đáp án B.
Câu 14:
Phép chia x3 + x2 - 4x + 7 cho x2 - 2x + 5 được đa thức dư là ?
Ta có phép chia
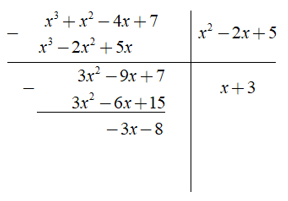
Dựa vào kết quả của phép chia trên,, ta có đa thức dư là - 3x - 8.
Chọn đáp án B.
Câu 15:
Giá trị của x thỏa mãn 2x( x + 3 ) + 2( x + 3 ) = 0 là ?
Ta có 2x( x + 3 ) + 2( x + 3 ) = 0 ⇔ ( x + 3 )( 2x + 2 ) = 0
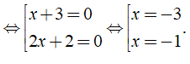
Chọn đáp án C.
Câu 16:
Tính ( x + )( x - )( 9 - 18x ) ta được kết quả ?
Ta có: ( x + )( x - )( 9 - 18x ) = ( x2 - )( 9 - 18x ) = x2( 9 - 18x ) - ( 9 - 18x )
= 9x2 - 18x3 - 1 + 2x = - 18x3 + 9x2 + 2x - 1.
Chọn đáp án A.
Câu 17:
Ta có:
( 2x + y )2 + ( 2x - y )2 = 4x2 + 4xy + y2 + 4x2 - 4xy + y2 = 8x2 + 2y2.
Chọn đáp án B.
Câu 18:
Rút gọn biểu thức xn( xn + 1 + yn ) - yn( xn + yn - 1 ) được kết quả là?
Ta có:
xn( xn + 1 + yn ) - yn( xn + yn - 1 ) = xn.xn + 1 + xn.yn - yn.xn - yn.yn - 1
= x2x + 1 + xn.yn - xn.yn - y2n - 1 = x2x + 1 - y2n - 1.
Chọn đáp án A.
Câu 19:
Rút gọn biểu thức ( a - b )3 + ( a + b )3 - a( 6b2 + 2a2 ) được kết quả là ?
Ta có:
( a - b )3 + ( a + b )3 - a( 6b2 + 2a2 ) = a3 - 3a2b + 3ab2 - b3 + a3 + 3a2b + 3ab2 + b3 - 6ab2 - 2a3
= 2a3 + 6ab2 - 6ab2 - 2a3 = 0.
Chọn đáp án D.
Câu 20:
Ta có P = x3 - 9x2 + 27x - 17 = ( x3 - 9x2 + 27x - 27 ) + 10 = ( x - 3 )3 + 10.
Với x =4, ta có: P = ( 4 - 3 )3 + 10 = 1 + 10 = 11.
Chọn đáp án C.
Câu 21:
Giá trị của biểu thức M = ( x - y + z )2 + ( z - y )2 + 2( x - y + z )( y - z ) tại x =10 là ?
Ta có: M = ( x - y + z )2 + ( z - y )2 + 2( x - y + z )( y - z )
= ( x - y + z )2 - 2( x - y + z )( z - y ) + ( z - y )2
= [ ( x - y + z ) - ( z - y ) ]2 = x2
Với x =10, ta có P = 102 = 100.
Chọn đáp án C.
Câu 22:
Thu gọn ( a + b - c )7:( a + b - c )5, ta được kết quả ?
Ta có ( a + b - c )7:( a + b - c )5 = ( a + b - c )7 - 5 = ( a + b - c )2
Chọn đáp án A.
Câu 23:
Phân tích đa thức 3x + 6xy + 2yz + z thành nhân tử, ta được:
Ta có: 3x + 6xy + 2yz + z = ( 3x + 6xy ) + ( 2yz + z )
= 3x( 2y + 1 ) + z( 2y + 1 ) = ( 2y + 1 )( 3x + z ).
Chọn đáp án A.
Câu 24:
Chọn câu sai với mọi số tự nhiên n thì giá trị của biểu thức ( n + 7 )2 - ( n - 5 )2 chia hết cho ?
Ta có: ( n + 7 )2 - ( n - 5 )2 = ( n2 + 14n + 49 ) - ( n2 - 10n + 25 ) = 24n + 24
Khi đó ta có:

⇒ 24n + 24 chia hết cho 24,8,6.
Do đó 24n + 24 không chia hết cho 16.
Chọn đáp án B.
Câu 25:
Ta có 16x4 - 40x2y3 + 25y6 = ( 4x2 )2 - 2.( 4x2 ).( 5y3 ) + ( 5y3 )2 = ( 4x2 - 5y3 )2
Nhận thấy: ( 4x2 - 5y3 )2 ≥ 0 ⇒ Giá trị của biểu thức là một số không âm.
Chọn đáp án D.
Câu 26:
Để biểu thức 9x2 + 30x + a là bình phương của một tổng thì giá trị của a thỏa mãn yêu cầu là ?
Ta có: 9x2 + 30x + a = ( 3x )2 + 2.( 3x ).5 + 52 + a - 25 = ( 3x + 5 )2 + a - 25
Để biểu thức 9x2 + 30x + a là bình phương của một tổng ⇔ a - 25 = 0 ⇔ a = 25.
Chọn đáp án B.
Câu 27:
Ta có: y = ( x - 3 )2 + 1 ≥ 1 vì ( x - 3 )2 ≥ 0.
⇒ Min = 1 khi x - 3 = 0 ⇔ x = 3.
Chọn đáp án A.
Câu 28:
Giá trị nhỏ nhất của biểu thức 9x2 - 6x + 5 đạt được khi x bằng ?
Ta có: 9x2 - 6x + 5 = ( 9x2 - 6x + 1 ) + 4 = ( 3x - 1 )2 + 4 ≥ 4 vì ( 3x - 1 )2 ≥ 0
⇒ Min = 4 khi và chỉ khi 3x - 1 = 0 ⇔ x = .
Chọn đáp án B.
Câu 29:
Giá trị lớn nhất của biểu thức S = 4x - 2x2 + 1 là ?
Ta có S = 4x - 2x2 + 1 = - 2x2 + 4x + 1 = - 2( x2 - 2x ) + 1
= - 2( x2 - 2x + 1 ) + 2 + 1 = - 2( x - 1 )2 + 3 ≤ 3. vì - 2( x - 1 )2 ≤ 0∀ x
⇒ Min = 3 khi và chỉ khi x - 1 = 0 ⇔ x = 1.
Chọn đáp án A.
Câu 30:
Giá trị của 2x2 + 3( x + 1 )( x - 1 ) = 5x( x + 1 ) thỏa mãn
Ta có 2x2 + 3( x + 1 )( x - 1 ) = 5x( x + 1 )
⇔ 2x2 + 3( x2 - 1 ) = 5x2 + 5x
⇔ 5x2 - 3 = 5x2 + 5x ⇔ 5x = - 3 ⇔ x = - .
Chọn đáp án D.
Câu 31:
Thực hiện các phép tính sau
a, ( x2 -1 )( x2 + 2x )
a) Ta có: ( x2 -1 )( x2 + 2x ) = x2( x2 + 2x ) - ( x2 + 2x )
= x4 + 2x3 - x2 - 2x.
Câu 32:
b) Ta có ( x + 3 )( x2 + 3x -5 ) = x( x2 + 3x -5 ) + 3( x2 + 3x -5 )
= x3 + 3x2 - 5x + 3x2 + 9x - 15 = x3 + 6x2 + 4x - 15
Câu 33:
Thực hiện các phép tính sau:
c, ( x -2y )( x2y2 - xy + 2y )
c) Ta có ( x -2y )( x2y2 - xy + 2y ) = x( x2y2 - xy + 2y ) - 2y( x2y2 - xy + 2y )
= x3y2 - x2y + 2xy - 2x2y3 + 2xy2 - 4y2
Câu 34:
Thực hiện phép tính sau
d, ( 1/2xy -1 )( x3 -2x -6 )
d) Ta có ( xy -1 )( x3 -2x -6 ) = xy( x3 -2x -6 ) - ( x3 -2x -6 )
= x4y - x2y - 3xy - x3 + 2x + 6
Câu 35:
a, xy( xy2 + y3 )
a) Ta có: xy( xy2 + y3 ) = xy.xy2 + xy.y3 = x2y3 + xy4.
Câu 36:
b, 2y( x + yz + zx )
b) Ta có: 2y( x + yz + zx ) = 2y.x + 2y.yz + 2y.zx = 2xy + 2y2z + 2xyz
Câu 38:
Tính giá trị của các biểu thức sau:
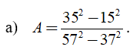
a) Ta có
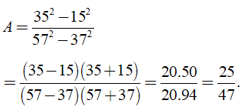
(áp dụng hằng đẳng thức a2 - b2 = ( a + b )( a - b ) )
Vậy A= 25/47
Câu 39:
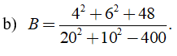
b) Ta có
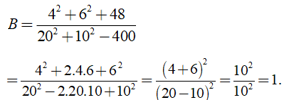
(áp dụng hằng đẳng thức ( a + b )2 = a2 + 2ab + b2;( a - b )2 = a2 - 2ab + b2 )
Vậy B=1
Câu 40:
Phân tích các đa thức sau thành nhân tử
a, ( ab - 1 )2 + ( a + b )2
a) Ta có ( ab - 1 )2 + ( a + b )2 = a2b2 - 2ab + 1 + a2 + 2ab + b2
= a2b2 + a2 + b2 + 1 = ( a2b2 + a2 ) + ( b2 + 1 )
= a2( b2 + 1 ) + ( b2 + 1 ) = ( a2 + 1 )( b2 + 1 )
Câu 41:
b) Ta có x3 + 2x2 + 2x + 1 = ( x3 + 1 ) + ( 2x2 + 2x )
= ( x + 1 )( x2 - x + 1 ) + 2x( x + 1 ) = ( x + 1 )( x2 + x + 1 )
Câu 42:
c) Ta có x2 - 2x - 4y2 - 4y = ( x2 - 4y2 ) - ( 2x + 4y )
= ( x - 2y )( x + 2y ) - 2( x + 2y )
= ( x + 2y )( x - 2y - 2 ).
Câu 43:
Tính giá trị của biểu thức sau A = x6 - 2x4 + x3 + x2 - x, biết x3 - x = 6.
Ta có: A = x6 - 2x4 + x3 + x2 - x = ( x6 - 2x4 + x2 ) + ( x3 - x )
= ( x3 - x )2 + ( x3 - x )
Với x3 - x = 6, ta có A = 62 - 6 = 36 - 6 = 30.
Vậy A = 30.
Câu 44:
Tính giá trị của các biểu thức sau
a, P = 12x4y2:( - 9xy2 ) tại x = - 3;y = 1,005.
a) Ta có P = 12x4y2:( - 9xy2 ) = ()x4 - 1y2 - 2 = - x3
Với x = - 3;y = 1,005 ta có P = - ( - 3 )3 = 36.
Vậy P = 36.
Câu 45:
b, Q = 3x4y3:2xy2 tại x = 2;y = 1.
b) Ta có Q = 3x4y3:2xy2 = x4 - 1y3 - 2 = x3y.
Với x = 2; y = 1 ta có Q = ( 2 )3.1 = 12.
Vậy Q = 12.
Câu 46:
Tìm biết
a, 4( 18 - 5x ) - 12( 3x - 7 ) = 15( 2x - 16 ) - 6( x + 14 )
a) Ta có 4( 18 - 5x ) - 12( 3x - 7 ) = 15( 2x - 16 ) - 6( x + 14 )
⇔ 4.18 - 4.5x - 12.3x - 12.( - 7 ) = 15.2x - 15.16 - 6.x - 6.14
⇔ 156 - 56x = 24x - 324 ⇔ 56x + 24x = 156 + 324
⇔ 80x = 480 ⇔ x = 6.
Vậy giá trị x cần tìm là x = 6.
Câu 47:
b, 2( 5x - 8 ) - 3( 4x - 5 ) = 4( 3x - 4 ) + 11.
b) Ta có 2( 5x - 8 ) - 3( 4x - 5 ) = 4( 3x - 4 ) + 11
⇔ 2.5x - 2.8 - 3.4x - 3.( - 5 ) = 4.3x - 4.4 + 11
⇔ - 2x - 1 = 12x - 5 ⇔ 12x + 2x = - 1 + 5
⇔ 14x = 4 ⇔ x = .
Vậy giá trị x cần tìm là x =
Câu 48:
c, ( x + 2 )( x + 3 ) - ( x - 2 )( x + 5 ) = 6
c) Ta có ( x + 2 )( x + 3 ) - ( x - 2 )( x + 5 ) = 6
⇔ x( x + 3 ) + 2( x + 3 ) - x( x + 5 ) + 2( x + 3 ) = 6
⇔ x2 + 3x + 2x + 6 - x2 - 5x + 2x + 6 = 6
⇔ 2x = - 6 ⇔ x = - 3.
Vậy giá trị x cần tìm là x = -3
Câu 49:
d, 3( 2x - 1 )( 3x - 1 ) - ( 2x - 3 )( 9x - 1 ) = 0
d) Ta có 3( 2x - 1 )( 3x - 1 ) - ( 2x - 3 )( 9x - 1 ) = 0
⇔ 3( 6x2 - 2x - 3x + 1 ) - ( 18x2 - 2x - 27x + 3 ) = 0
⇔ 18x2 - 15x + 3 - 18x2 + 29x - 3 = 0
⇔ 14x = 0 ⇔ x = 0
Vậy giá trị x cần tìm là x =0
Câu 50:
Chứng mình rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = x2y3:( - xy ) + 2x( y - 1 )( y + 1 )
Ta có A = x2y3:( - xy ) + 2x( y - 1 )( y + 1 ) = - 2x2 - 1y3 - 1 + 2x( y - 1 )( y + 1 )
= - 2xy2 + 2x( y2 - 1 ) = - 2xy2 + 2xy2 - 2x = - 2x
⇒ Giá trị của biểu thức A không phụ thuộc vào biến y
Câu 51:
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7xn - 1y5 - 5x3y4;
B = 5x2yn
Ta có A:B = ( 7xn - 1y5 - 5x3y4 ):( 5x2yn ) = xn - 3y5 - n - xy4 - n
Theo đề bài đa thức A chia hết cho đơn thức B
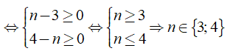
Vậy giá trị n cần tìm là n∈ {3; 4}
Câu 52:
Tìm các số nguyên n để giá trị của biểu thức n3 + 6n2 -7n + 4 chia hết cho giá trị của biểu thức n-2
Ở đây, ta có thực hiện đặt phép chia như câu 1 để tìm số dư và tìm điều kiện giá trị của n để thỏa mãn đề bài. Nhưng bài này ta làm cách biến đội như sau:
Ta có n3 + 6n2 -7n + 4 = ( n3 - 3n2.2 + 3.n.22 - 8 ) + 12n2 - 19n + 12
= ( n - 2 )3 + 12n( n - 2 ) + 5( n - 2 ) + 22
Khi đó ta có: (n3 + 6n2 - 7n + 4)/n - 2 = ( n - 2 )2 + 12n + 5 + 22/(n - 2)
Để giá trị của biểu thức n3 + 6n2 -7n + 4 chia hết cho giá trị của biểu thức n -2
⇔ ( n - 2 ) ∈ ƯCLN( 22 ) = {± 1; ± 2; ± 11; ± 22}
⇒ n ∈ {- 20; - 9;0;1;3;4;13;24}
Vậy các giá trị nguyên của n cần tìm là n ∈ {- 20; - 9;0;1;3;4;13;24}
Câu 53:
Chứng tỏ rằng các biểu thức sau không phụ thuộc vào biến x
a, x( 2x + 1 ) - x2( x + 2 ) + ( x3 - x + 3 )
b) Ta có: 4( x - 6 ) - x2( 2 + 3x ) + x( 5x - 4 ) + 3x2( x - 1 )
= ( 4x - 24 ) - ( 2x2 + 3x3 ) + ( 5x2 - 4x ) + ( 3x3 - 3x2 )
= 4x - 24 - 2x2 - 3x3 + 5x2 - 4x + 3x3 - 3x2 = - 24.
Biểu thức không phụ thuộc vào giá trị của biến x.
Câu 54:
b, 4( x - 6 ) - x2( 2 + 3x ) + x( 5x - 4 ) + 3x2( x - 1 )
b) Ta có: 4( x - 6 ) - x2( 2 + 3x ) + x( 5x - 4 ) + 3x2( x - 1 )
= ( 4x - 24 ) - ( 2x2 + 3x3 ) + ( 5x2 - 4x ) + ( 3x3 - 3x2 )
= 4x - 24 - 2x2 - 3x3 + 5x2 - 4x + 3x3 - 3x2 = - 24.
Biểu thức không phụ thuộc vào giá trị của biến x.
Câu 55:
Chứng minh rằng: ( a + b )2 - ( a - b )2 = 4ab.
Từ đó tính:
a, ( a + b )2 biết a - b = 3 và ab = 4.
Ta có :
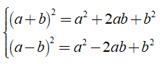
⇒ ( a + b )2 - ( a - b )2 = ( a2 + 2ab + b2 ) - ( a2 - 2ab + b2 )
⇒ ( a + b )2 - ( a - b )2 = 4ab.
a) Ta có ( a + b )2 - ( a - b )2 = 4ab ⇔ ( a + b )2 = ( a - b )2 + 4ab
Với a - b = 3 và ab = 4, ta có: ( a + b )2 = 32 + 4.4 = 25.
Câu 56:
b) Ta có: ( a + b )2 - ( a - b )2 = 4ab ⇔ ( a - b )2 = ( a + b )2 - 4ab
Với a + b = 6 và ab = 8, ta có: ( a - b )2 = 62 - 4.8 = 36 - 32 = 4.
Câu 57:
Phân tích đa thức sau thành nhân tử
a, a3 + b3 + c3 - 3abc
a) Ta có a3 + b3 + c3 - 3abc = ( a3 + 3a2b + 3ab2 + b3 ) + c3 - 3ab( a + b ) - 3abc
= ( a + b )3 + c3 - 3ab( a + b + c )
= [ ( a + b )3 + 3( a + b )2c + 3( a + b )c2 + c3 ] - 3( a + b )c( a + b + c ) - 3ab( a + b + c )
= ( a + b + c )3 - 3( a + b + c )( ab + bc + ca )
= ( a + b + c )[ ( a + b + c )2 - 3( ab + bc + ca ) ]
= ( a + b + c )( a2 + b2 + c2 - ab - bc - ca )
Câu 58:
b) Ta có z - x = - [ ( y - z ) + ( x - y ) ]
Khi đó ta có: x2( y - z ) + y2( z - x ) + z2( x - y )
= x2( y - z ) - y2[ ( y - z ) + ( x - y ) ] + z2( x - y )
= ( y - z )( x2 - y2 ) - ( x - y )( y2 - z2 )
= ( y - z )( x - y )( x + y ) - ( x - y )( y + z )( y - z )
= ( y - z )( x - y )( x + y - y - z ) = ( y - z )( x - y )( x - z )
Câu 59:
Thực hiện các phép chia sau
a, [ 7( x2 - 1 )4 + 2( 1 - x )3 - 3( x - 1 )2 ]:2( x - 1 )2
a) Ta có [ 7( x2 - 1 )4 + 2( 1 - x )3 - 3( x - 1 )2 ]:2( x - 1 )2
= [ 7( x - 1 )4( x + 1 )4 - 2( x - 1 )3 - 3( x - 1 )2 ]:2( x - 1 )2
= ( x - 1 )2( x + 1 )4 - ( x - 1 ) -
Câu 60:
b) Ta có [ 5( x3 - y3 )4 + ( x - y )3 ]:( x2 - 2xy + y2 )
= [ 5( x - y )4( x2 + xy + y2 )4 + ( x - y )3 ]:( x - y )2
= 5( x - y )2( x2 + xy + y2 )4 + ( x - y )
Câu 61:
Tìm giá trị của a để biểu thức ( a2x3 + 3ax2 - 6x - 2a ) chia hết cho ( x + 1 )
Do ( a2x3 + 3ax2 - 6x - 2a ) chia hết cho ( x + 1 ) nên ta có thể viết như sau:
( a2x3 + 3ax2 - 6x - 2a ) = ( mx2 + nx + p )( x + 1 ) ( 1 )
Trong đó thương ( mx2 + nx + p ) là một tam thức bậc ha.
Ta thấy ( 1 ) đúng với mọi giá trị của x, nên cũng đúng với x = - 1
Do đó ta có: - a2 + 3a + 6 - 2a = 0 ⇔ - a2 + a + 6 = 0⇔
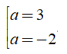
Vậy để ( a2x3 + 3ax2 - 6x - 2a ) chia hết cho ( x + 1 ) thì giá trị của a là a =3 hoặc a = -2
Câu 62:
Tìm giá trị của m để đa thức ( x3 + 3x2 - 5x + m ) chia hết cho ( x - 2 )
Tìm giá trị của m để đa thức ( x3 + 3x2 - 5x + m ) chia hết cho ( x - 2 )
Hướng dẫn giải:
Nhận xét: Ở đây, ta có thể đặt phép chia của ( x3 + 3x2 - 5x + m ) cho ( x - 2 ) để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán.
Ta có: ( x3 + 3x2 - 5x + m ) = ( x3 - 2x2 ) + ( 5x - 10 ) + m + 10
= x2( x - 2 ) + 5( x - 2 ) + m + 10
Nhận thấy:
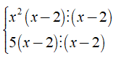
Khi đó để ( x3 + 3x2 - 5x + m ) cho ( x - 2 ) khi và chỉ khi m + 10 = 0 ⇔ m = - 10.
Vậy m = - 10 là giá trị cần tìm.
