Bài tập Hình hộp chữ nhật (tiếp-có lời giải chi tiết)
-
752 lượt thi
-
9 câu hỏi
-
10 phút
Danh sách câu hỏi
Câu 1:
Quan sát hình hộp chữ nhật ở hình 75:
- Hãy kể tên các mặt của hình hộp.
- BB’ và AA’ có cùng nằm trong một mặt phẳng hay không ?
- BB’ và AA’ có điểm chung hay không ?
- Các mặt: (ABCD), (A’B’C’D’), (ABB’A’), (CDD’C’), (ADD’A’), (BCC’B’)
- BB’ và AA’ có cùng nằm trong một mặt phẳng là (ABB’A’)
- BB’ và AA’ không có điểm chung
Câu 2:
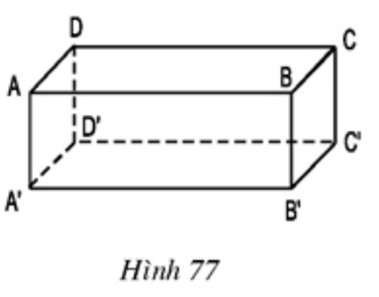
Quan sát hình hộp chữ nhật ở hình 77:
- AB có song song với A’B’ hay không ? Vì sao ?
- AB có nằm trong mặt phẳng (A’B’C’D’) hay không ?
- AB có song song với A’B’ vì là hai cạnh đối nhau của hình chữ nhật ABB’A’
- AB không nằm trong mặt phẳng (A’B’C’D’)
Câu 3:
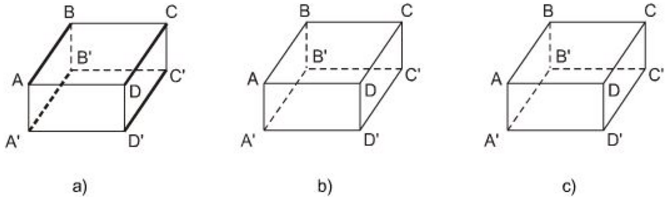
Người ta tô đậm những cạnh song song và bằng nhau của một hình hộp chữ nhật như ở hình 80a. Hãy thực hiện điều đó với hình 80b và 80c.
Hình 80
Các cạnh song song và bằng nhau của một hình hộp chữ nhật trên hình 80b, 80c là:
+ BC = B'C' = AD = A'D'
+ AA’ = BB’ = CC’ = DD’
Câu 4:
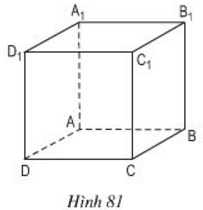
ABCD.A1B1C1D1 là một hình lập phương (h.81). Quan sát hình và cho biết:
a) Những cạnh nào song song với cạnh C1C?
b) Những cạnh nào song song với A1D1?
a) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD
Câu 5:
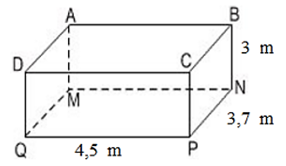
Một căn phòng dài 4,5m, rộng 3,7m và cao 3,0m.
Người ta muốn quét vôi trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là 5,8. Hãy tính diện tích cần quét vôi.
Phân tích đề
Tưởng tượng căn phòng là một hình hộp chữ nhật ABCD.MNPQ trong đó:
- Trần nhà là hình chữ nhật ABCD.
- Bốn bức tường là 4 hình chữ nhật: ABNM ; CPQD; BNPC ; QDAM
- Khi đó diện tích quét vôi = diện tích trần + diện tích 4 bức tường – diện tích cửa.
Lời giải:
- Diện tích trần nhà:
4,5 x 3,7 = 16,65 ()
- Diện tích bốn bức tường (hay còn gọi là diện tích xung quanh):
2.4,5.3 + 2.3.3,7 = 2.(4,5 + 3,7).3 = 49,2 ()
Vì SAMQD = SBNPC = 3.3,7 nên SAMQD + SBNPC = 2.3.3,7
Và SABNM = SDCPQ = 4,5.3 nên SABNM + SDCPQ = 2.4,5.3
- Diện tích cần được quét vôi:
16,65 + 49,2 – 5,8 = 60,05 ()
Câu 6:
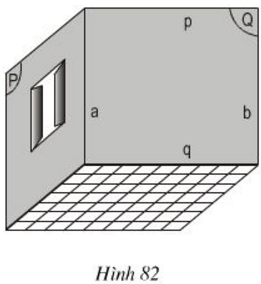
Hình 82 vẽ một phòng ở. Quan sát hình và giải thích vì sao:
a) Đường thẳng b song song với mp(P)?
b) Đường thẳng p song song với sàn nhà?
a) Ta có b không thuộc mặt phẳng (P) và b // a, a nằm trong (P). Nên b// (P).
b) Ta có p không thuộc sàn nhà và đường thẳng p song song với đường thẳng q trong sàn nhà nên p song song với sàn nhà.
Câu 7:
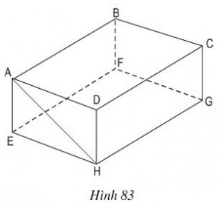
Hình hộp chữ nhật ABCD.EFGH (h.83) có cạnh AB song song với mp(EFGH).
a) Hãy kể tên các cạnh khác song song với mặt phẳng (EFGH).
b) Cạnh CD song song với những mặt phẳng nào của hình hộp chữ nhật?
c) Đường thẳng AH không song song với mặt phẳng (EFGH), hãy chỉ ra mặt phẳng song song với đường thẳng đó.
a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).
Câu 8:
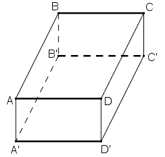
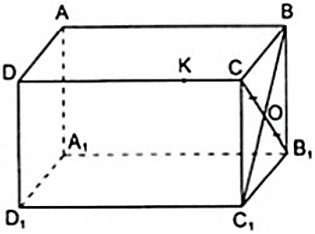
Cho hình hộp chữ nhật ABCD.
a) Nếu O là trung điểm của đoạn CB1 thì O có là điểm thuộc đoạn BC1 ?
b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB1 hay không?
a) Câu trả lời trên là có. Thật vậy, vì mặt bên BCC1B1 là hình chữ nhật có O là trung điểm của đường chéo CB1 nên O cũng là trung điểm của đường chéo BC1 (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn BC1.
b) K không thuộc cạnh BB1 vì K ∉ mp( BB1C1C ) mà BB1 thuộc mặt phẳng đó
Vậy K không thuộc cạnh BB1.
Câu 9:
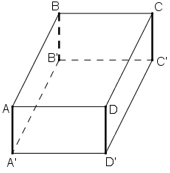
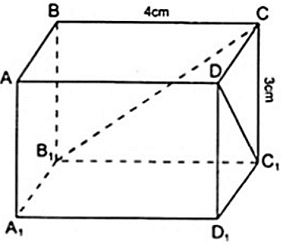
Các kích thước của hình hộp chữ nhật ABCD.A1B1C1D1 là DC = 5 cm; CB = 4cm; BB1 = 3 cm. Tính các độ dài DC1, CB1 ?
DC1 ∈ mp( DCC1D1 ) với là hình chữ nhật nên Δ DCC1 vuông tại C.
Áp dụng định lý Py – ta – go vào Δ DCC1 vuông tại C ta được: DC12 = CC12 + CD2
Hay DC12 = 32 + 52 ⇔ DC12 = 34 ⇔ DC1 = ( cm )
CB1 ∈ ( BCC1B1 ) là hình chữ nhật nên Δ BCB1 vuông tại B.
Áp dụng định lí Py – ta – go vào Δ BCB1 vuông tại B ta được: CB12 = CB2 + BB12
Hay CB12 = 32 + 42 = 52 ⇔ CB1 = 5( cm )
Vậy DC1 = (cm ); CB1 = 5(cm)