Trắc nghiệm chuyên đề Toán 8 Chủ đề 10: Đường thẳng song song với một đường thẳng cho trước có đáp án
Trắc nghiệm chuyên đề Toán 8 Chủ đề 10: Đường thẳng song song với một đường thẳng cho trước có đáp án
-
272 lượt thi
-
4 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho Δ ABC có D là trung điểm của AB, kẻ DE//BC ( E AC ). Chứng minh rằng AE = EC.
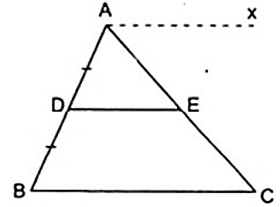
Do DE//BC theo giả thiết nên vẽ thêm Ax//DE thì
Ax//DE//BC ( 1 )
Vì D là trung điểm của AB nên AD = BD ( 2 )
Từ ( 1 ), ( 2 ) suy ra ba đường Ax, DE, BC là ba đường song song cách đều nên nó chắn trên đường thẳng AC hai đoạn thẳng liên tiếp bằng nhau là AE = EC.
Câu 2:
Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K lần lượt là các chân đường cao kẻ từ kẻ từ B và C đến đường thẳng DE. Chứng minh rằng HE = DK.
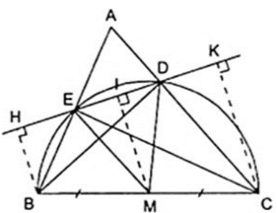
Vì BD, CE là đường cao của tam giác ABC nên
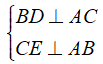
do đó Δ BDC vuông tại D, Δ CEB vuông tại E.
Gọi M là trung điểm của BC
⇒ DM, EM là đường trung tuyến ứng với cạnh huyền của Δ BDC và Δ CEB.
Áp dụng tính chất của đường trung tuyến ứng với cạnh huyền của hai tam giác trên ta được:
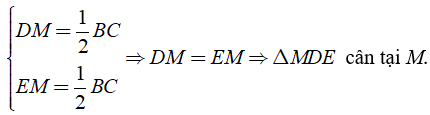
Từ giả thiết ta có tứ giác BHKC là hình thang vuông nên vẽ MI ⊥ DE thì BH//MI//CK ( 1 ) (vì cùng vuông góc với đường thẳng DE)
Mà ta có BM = MC ( 2 ) (do ta vẽ hình trên)
Từ ( 1 ),( 2 ) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK ( 3 ).
Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được:
EI = ID ( 4 )
Trừ theo vế đẳng thức ( 3 ) cho ( 4 ), ta được: HE = DK.
Câu 3:
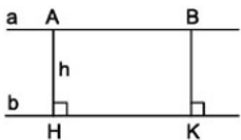
Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia. h là khoảng cách giữa hai đường thẳng song song a và b.
Câu 4:
Cho hình dưới đây, trong đó các đường thẳng a,b,c,d song song với nhau. Nếu các đường thẳng a,b,c,d song song cách đều thì :
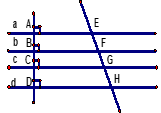
Định lí:
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
