Dạng 1: Phương pháp giải bài toán có đáp án
-
430 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
a.
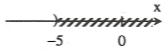
Ta có
Vậy, nghiệm của bất phương tình là x < -5 và ta có biểu diễn.
Câu 2:
b.
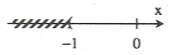
Ta có:
Vậy, nghiệm của bất phương tình là x > -1 và ta có biểu diễn.
Câu 3:
a. Ta có biến đổi:
Vậy, nghiệm của bất phương trình là x > 3.
Câu 7:
Giải các bất phương trình sau:
a. Ta có biến đổi:
Vậy, nghiệm của bất phương trình là x > -9.
Câu 13:
Biến đổi phương trình về dạng:
Vậy, bất phương trình có nghiệm x < 3.
Câu 14:
Giải bất phương trình:
Ta có thể lựa chọn một trong hai cách giải sau:
Cách 1: Nhân hai vế của bất phương trình với 24, được:
Vậy, bất phương trình có nghiệm x > 3.
Cách 2: Biến đổi bất phương trình về dạng:
Vậy, bất phương trình có nghiệm x > 3.
Câu 15:
Giải các bất phương trình sau:
a. Ta có biến đổi:
Vậy, nghiệm của bất phương trình là x < 0.
Câu 19:
Cho biểu thức: .
Tìm các giá trị của x sao cho giá trị A lớn hơn -1 nhưng nhỏ hơn 1. Biểu diễn trên trục số các giá trị tìm được của x.
Trước tiên ta đi rút gọn biểu thức A:
- Để A > -1 điều kiện là:
- Để A < 1 điều kiện là:
.
Vậy, để có được -1 < A < 1 điều kiện là và ta có biểu diễn:
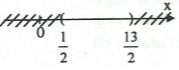
Cách biểu diễn trên trục được thực hiện như sau:
1. Xác định vị trí của các điểm và
2. Giữ nguyên đoạn thẳng từ điểm đến điểm .
3. Gạch chéo phần còn lại, gạch cả điểm và
.
Câu 20:
Trong cuộc thi bắn súng, mỗi xạ thủ được bắn 10 phát. Mỗi lần trúng đích được 5 điểm, mỗi lần trượt bị trừ 1 điểm. Xạ thủ nào đạt được 30 điểm trở lên thì được thưởng. Hỏi xạ thủ phải bắn trúng đích bao nhiêu lần thì được thưởng?
Gọi số lần bắn trúng đích là x, điều kiện (*)
Theo giả thiết:
- Mỗi hạ thủ được bắn 10 phát nên số lần bắn trượt là , khi đó tổng số điểm đạt được là .
- Muốn được thưởng, tổng số điểm phải đạt từ 30 điểm trở lên, do đó:
Kết hợp với điều kiện (*), ta được:
.
Vậy, để nhận được thưởng thì số lần bắn trúng đích phải là 7 lần, hoặc 8 lần, hoặc 9 lần, hoặc 10 lần.
