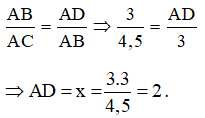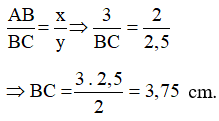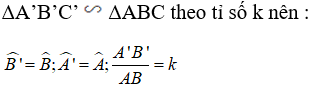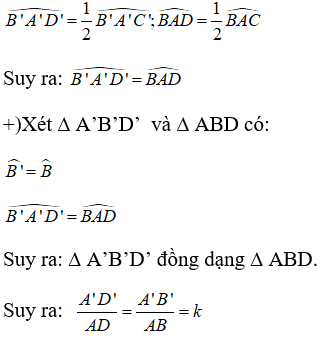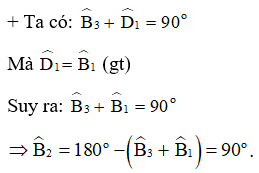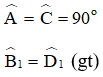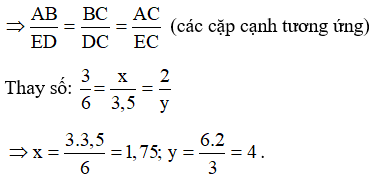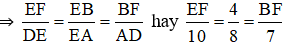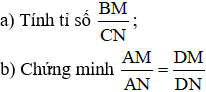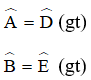16 câu hỏi trắc nghiệm thuộc Bài tập Trường hợp đồng dang thứ ba (có lời giải chi tiết)

Câu 1:

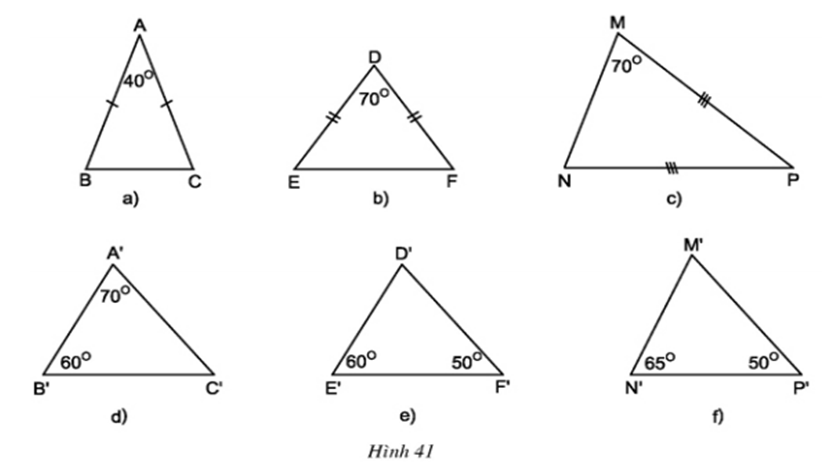
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)

Xem đáp án

- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A

Mà ΔABC cân tại A ⇒ ∠B = ∠C

⇒∠B = ∠C = ( 180o- 40o)/2 = 70o

ΔMNP cân tại P ⇒ ∠M = ∠N = 70o

ΔABC và ΔPMN có

∠B = ∠M = 70o)

∠C = ∠N = 70o)

⇒ ΔABC ∼ ΔPMN (g.g)

- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o

⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o

ΔA’B’C’ và ΔD’E’F’ có

∠B' = ∠E' (= 60o)

∠C' = ∠F' (= 50o)

⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)

Câu 2:

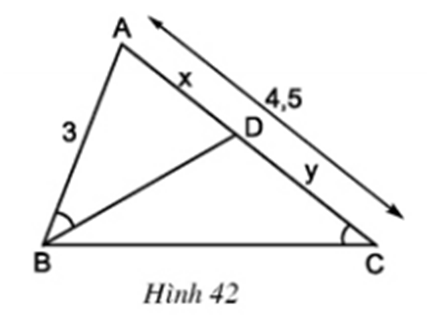
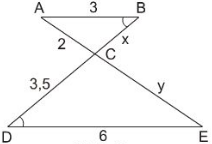
Ở hình 42 cho biết AB = 3cm; AC = 4,5cm và ∠(ABD) = ∠(BCA).

a) Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?

b) Hãy tính các độ dài x và y (AD = x, DC = y).

c) Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD.

Xem đáp án

a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC

ΔABD và ΔACB có

∠B = ∠C

∠A chung

⇒ ΔABD ∼ ΔACB (g.g)

b) Theo a ta có :

c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:

Câu 3:

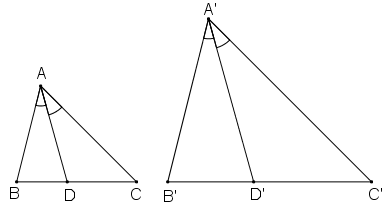
Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k.

Xem đáp án

Gọi AD và A’D' lần lượt là hai đường phân giác của ΔABC và ΔA'B'C'.

+) Lại có; AD, A’D’ lần lượt là phân giác của góc A và góc A’ nên:

Câu 4:

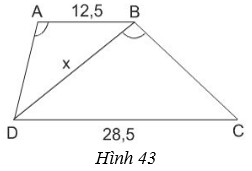
Tính độ dài x của đoạn thẳng BD trong hình 43 (làm tròn đến chữ số thập phân thứ nhất), biết rằng ABCD là hình thang (AB // CD); AB = 12,5cm, CD = 28,5cm, góc DAB = góc DBC.

Xem đáp án

Vậy x ≈ 18,87 cm.

Câu 5:

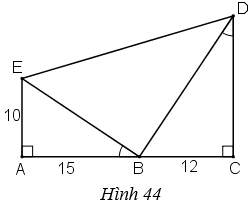
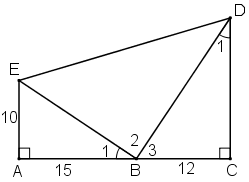
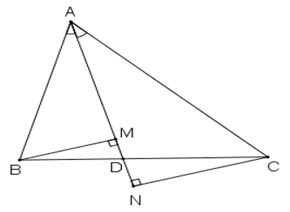
Hình 44 cho biết góc EBA = góc BDC.

a) Trong hình vẽ có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD, BE, BD và ED (làm tròn đến chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác BDE với tổng diện tích của hai tam giác AEB và BCD.

Xem đáp án

a) + ΔABE vuông tại A.

+ ΔBCD vuông tại C.

+ Ta có:

Vậy ΔBED vuông tại B.

b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:

+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:

Câu 6:

Tính độ dài x, y của các đoạn thẳng trong hình 45.

Hình 45

Xem đáp án

Câu 7:

Cho tam giác ABC, trong đó AB = 15cm, AC = 20cm. Trên hai cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = 8cm, AE = 6cm. Hai tam giác ABC và ADE có đồng dạng với nhau không? Vì sao?

Xem đáp án

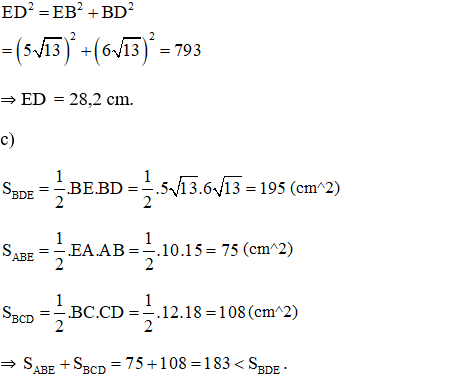
Câu 8:

Tìm các dấu hiệu để nhận biết hai tam giác cân đồng dạng.

Xem đáp án

+ Nếu cạnh bên và cạnh đáy của tam giác cân này tỉ lệ với cạnh bên và cạnh đáy của tam giác cân kia thì hai tam giác đó đồng dạng.

+ Nếu hai tam giác cân có hai góc ở đỉnh bằng nhau thì hai tam giác cân đồng dạng.

+ Nếu góc ở đáy của tam giác cân này bằng góc ở đáy của tam giác cân kia thì hai tam giác cân đó đồng dạng.

Câu 9:

So sánh các trường hợp đồng dạng của tam giác với các trường hợp bằng nhau của tam giác (nêu lên những điểm giống nhau và khác nhau).

Xem đáp án

So sánh:

Trường hợp	Giống nhau	Khác nhau
Trường hợp	Giống nhau	Bằng nhau	Đồng dạng
1	3 cạnh	3 cạnh tương ứng bằng nhau	3 cạnh tương ứng tỉ lệ
2	2 cạnh 1 góc	2 cạnh tương ứng và một góc kề với hai cạnh bằng nhau	2 cạnh tương ứng tỉ lệ
3	2 góc bằng nhau	1 cạnh và 2 góc kề tương ứng bằng nhau	Chỉ 2 góc bằng nhau, không cần có điều kiện cạnh

Câu 10:

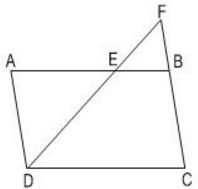
Cho hình bình hành ABCD (h.46) có độ dài các cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt cạnh CB kéo dài tại F.

a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng với nhau? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng.

b) Tính độ dài các đoạn thẳng EF và BF, biết rằng DE = 10cm.

Xem đáp án

a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.

ΔFCD có EB // CD (E ∈ FD, B ∈ FC)

⇒ ΔFEB ΔFDC (1)

ΔAED có FB // AD (F ∈ DE, B ∈ AE)

⇒ ΔFEB ΔDEA (2)

Từ (1) và (2) suy ra: ΔDEA ΔFDC (tính chất)

b) AB = 12cm, AE = 8cm

⇒ EB = AB – AE = 12 - 8 = 4cm.

Vì ABCD là hình bình hành nên AD = BC = 7cm

Do ΔFEB ΔDEA

⇒ EF = 5cm, BF = 3,5cm.

Câu 11:

Cho tam giác ABC có các cạnh AB = 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD.

Xem đáp án

Câu 12:

Hai tam giác ABC và DEF có góc A = góc D, góc B = góc E, AB = 8cm, BC = 10cm, DE =6cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm.

Xem đáp án

Câu 13:

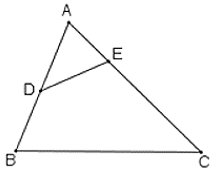
Cho hình bên biết AB = 6cm, AC = 9cm, $\hat{A B D} = \hat{B C A}$ . Độ dài đoạn AD là:

A. 2cm

B. 3cm

C. 4cm

D. 5cm

Xem đáp án

Xét ΔABD và ΔACB có:

$\hat{A}$ chung

$\hat{A B D} = \hat{B C A}$ (gt)

=> ΔABD ~ ΔACB (g-g)

$\Rightarrow \frac{A B}{A C} = \frac{A D}{A B} \Leftrightarrow \frac{6}{9} = \frac{x}{6} \Leftrightarrow x = \frac{6.6}{9} = 4 c m$

Đáp án: C

Câu 14:

Cho hình bên biết AB = 8cm, AC = 16cm, $\hat{A B D} = \hat{B C A}$ . Độ dài đoạn AD là:

A. 4cm

B. 8cm

C. 6cm

D. 5cm

Xem đáp án

Xét ΔABD và ΔACB có:

$\hat{A}$ chung

$\hat{A B D} = \hat{B C A}$ (gt)

=> ΔABD ~ ΔACB (g-g)

$\Rightarrow \frac{A B}{A C} = \frac{A D}{A B} \Leftrightarrow \frac{x}{8} = \frac{8}{16} \Leftrightarrow x = \frac{8.8}{16} = 4 c m$

Đáp án: A

Câu 15:

Nếu 2 tam giác ABC và DEF có $\hat{A} = 70 °, \hat{C} = 60 °, \hat{E} = 50 °, \hat{F} = 70 °$ thì chứng minh được:

A.ΔABC đồng dạng ΔFED

B. ΔACB đồng dạng ΔFED

C. ΔABC đồng dạng ΔDEF

D. ΔABC đồng dạng ΔDFE

Xem đáp án

Xét ΔABC có: $\hat{A} + \hat{B} + \hat{C}$ = $180^{\circ}$ $\Leftrightarrow 70^{\circ} + \hat{B} + 60^{\circ} = 180^{\circ}$

$\hat{B} = 180^{\circ} - 70^{\circ} - 60^{\circ} = 50^{\circ}$

Xét ΔABC và ΔFED có:

$\hat{A} = \hat{F} =$ $70^{\circ}$

$\hat{B} = \hat{E}$ = $50^{\circ}$

=> ΔABC ~ ΔFED (g - g)

Đáp án: A

Câu 16:

Cho 2 tam giác ABC và DEF có $\hat{A} = 40 °, \hat{C} = 80 °, \hat{E} = 40 °, \hat{F} = 60 °$ Chọn câu đúng.

A.ΔABC đồng dạng ΔDEF

B. ΔFED đồng dạng ΔCBA

C. ΔACB đồng dạng ΔEFD

D. ΔDFE đồng dạng ΔCBA

Xem đáp án

Xét ΔABC có: $\hat{A} + \hat{B} + \hat{C}$ = $180^{\circ}$ $\Rightarrow \hat{C} = 180^{\circ} - 40^{\circ} - 80^{\circ} = 60^{\circ}$

Tam giác DEF có: $\hat{D} + \hat{E} + \hat{F}$ = $180^{\circ}$ $\Rightarrow \hat{F} = 180^{\circ} - \hat{D} - \hat{E} = 180^{\circ} - 40^{\circ} - 60^{\circ} = 80^{\circ}$

Xét ΔABC và ΔFED có:

$\hat{A} = \hat{E}$ = $40^{\circ}$

$\hat{C} = \hat{D}$ = $60^{\circ}$

=> ΔABC đồng dạng ΔEFD (g - g) hay ΔCBA ~ ΔDFE

Đáp án: D

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Trường hợp đồng dang thứ ba (có lời giải chi tiết)

Bài tập Trường hợp đồng dang thứ ba (có lời giải chi tiết)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương