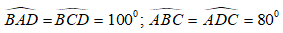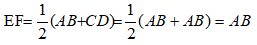Bài tập Hình bình hành (có lời giải chi tiết)
-
1103 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Chọn phương án sai trong các phương án sau?
Dấu hiệu nhận biết hình bình hành.
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
→ Đáp án C sai.
Chọn đáp án C.
Câu 2:
Chọn phương án đúng trong các phương án sau.
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
→ Đáp án C đúng.
Chọn đáp án C.
Câu 3:
Cho hình bình hành ABCD có , các góc còn lại của hình bình hành là?
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Câu 5:
Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
Trong hình bình hành các góc đối bằng nhau
Hay 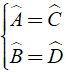
+ Δ ABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này
→ Đáp án B sai.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
→ Đáp án A sai vì theo giả thiết chưa đủ dữ kiện
+ Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên I là trung điểm của AC và BD nên BI là đường trung tuyến của Δ ABC
Chọn đáp án C.
Câu 6:
Cho tam giác ABC có M, N và P lần lượt là trung điểm AB, AC và BC. Tìm khẳng định sai ?
* Ta có M và N lần lượt là trung điểm của AB và AC
Suy ra: MN là đường trung bình của tam giác ABC.
⇒ MN // BC và MN = BC nên C đúng
* Vì M và P lần lượt là trung điểm của AB và BC nên MP là đường trung bình của tam giác ABC.
⇒ MP // AC nên B đúng
* Tứ giác MNCP có cạnh đối song song với nhau nên tứ giác MNCP là hình bình hành.
Nên đáp án D đúng
* Đáp án A sai vì AMNP không phải là tứ giác, phải là AMPN.
Chọn đáp án A
Câu 7:
Cho hình thang ABCD có AD// BC và . Tìm khẳng định sai
* Ta có:
Và 2 góc này ở vị trí trong cùng phía nên AB// CD (1)
* Lại có: AD// BC ( giả thiết) (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).
* Suy ra: AB = CD; AD = BC;
Vậy đáp án D sai vì hình bình hành chưa chắc đã có hai đường chéo bằng nhau.
Chọn đáp án D
Câu 8:
Cho hình bình hành ABCD, gọi E và F là trung điểm của AD và BC. Gọi I là giao điểm của AC và BD. Tìm khẳng định sai?
* Ta có ABCD là hình bình hành nên AB = CD; ABCD đồng thời là hình thang có 2 đáy là AB và CD.
Vì E và F lần lượt là trung điểm của AD và BC nên EF là đường trung bình của hình thang ABCD
Suy ra: EF// AB// CD và
(vì AB = CD)
* Xét tứ giác ABFE có AB// EF và AE// BF nên ABFE là hình bình hành
Tương tự, tứ giác EFCD là hình bình hành.
* Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.
Tam giác ACD có E và I lần lượt là trung điểm của AD và AC nên EI là đường trung bình của tam giác
Vì AC BD nên IA ID nên C sai.
Chọn đáp án C
Câu 9:
Cho hình bình hành ABCD có . Kẻ .Tìm khẳng định sai?
Ta có nên DH//CK.
Vì ABCD là hình bình hành nên AB//CD hay HK//CD.
Xét tứ giác HKCD có : DH // CK và HK // CD nên tứ giác HKCD là hình bình hành nên A đúng
Xét tam giác DHA và tam giác CKB là hai tam giác vuông có:
DH=CK (vì HKCD là hình bình hành)
AD=BC (vì ABCD là hình bình hành)
Suy ra DHA= CKB (ch.cgv) nên C đúng
Suy ra HA = KB (2 cạnh tương ứng) nên D đúng
Chọn đáp án B.