Trắc nghiệm chuyên đề Toán 8 Chủ đề 7: Hình bình hành có đáp án
-
280 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và .
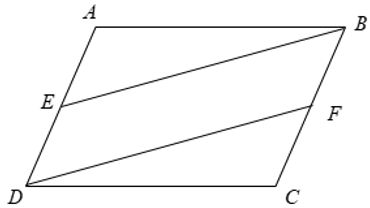
Xét tứ giác BEDF có
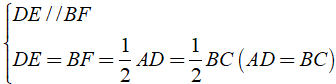
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên ( 1 )
BEDF là hình bình hành nên ( 2 )
Mà
Từ ( 2 ) và ( 3 ) ⇒ ( 4 )
Xét Δ ABE có = 1800 (5)
Xét Δ DFC có = 1800 (5)
Từ ( 1 ), ( 4 ), ( 5 ) ⇒ (đpcm)
Câu 2:
Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.
a) Chứng minh AHCK là hình bình hành.
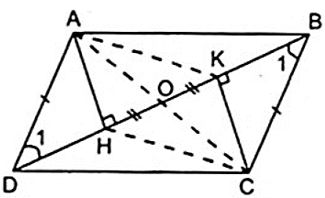
a) Từ giả thiết ta có:
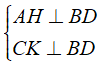
⇒ AH//CK. ( 1 )
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
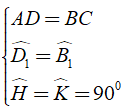
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
Câu 3:
b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.
b) Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường
Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
Câu 4:
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:
a) AK//CI
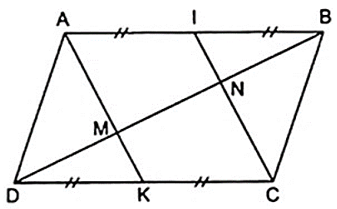
a) Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
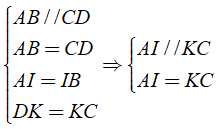
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
Câu 5:
b) DM = MN = NB
b) Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có:
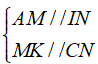
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
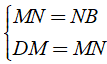
⇒ DM = MN = NB
Câu 6:
Dấu hiệu nhận biết hình bình hành.
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
→ Đáp án C sai.
Câu 7:
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
→ Đáp án C đúng.
Câu 8:

Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
⇒ = 1200.
Khi đó ta có:
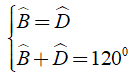
⇒ = 600
Câu 9:
Theo giả thiết, ta có: = 200 ⇒ + 200
Mặt khác ABCD là hình bình hành nên = 1800
Khi đó:
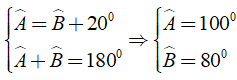
Câu 10:
Trong hình bình hành các góc đối bằng nhau
Hay
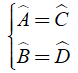
⇒ → đáp án D sai.
+ Δ ABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này
→ Đáp án B sai.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
→ Đáp án A sai vì theo giả thiết chưa đủ dữ kiện
