Trắc nghiệm Toán 8 Bài 3(có đáp án): Tính chất đường phân giác của tam giác
-
1014 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu đúng:
Vì AD là phân giác góc nên ta có: (tính chất đường phân giác của tam giác).
Đáp án: B
Câu 2:
Cho ΔABC, AD là phân giác trong của góc A. Hãy chọn câu sai:
Vì AD là phân giác góc nên ta có: (tính chất đường phân giác của tam giác).
hay B đúng
Lại có: => nên A đúng
=> nên D đúng
Chỉ có C sai
Đáp án: C
Câu 3:
Hãy chọn câu đúng. Tỉ số của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là cm.
Xét tam giác ABC, vì AD là phân giác góc nên ta có ó
Đáp án: A
Câu 4:
Cho hình vẽ, biết các số trên hình cùng đơn vị đo. Tỉ số bằng:
Xét tam giác ABC, vì AD là phân giác góc nên ta có ó
Đáp án: A
Câu 5:
Hãy chọn câu đúng. Tính độ dài x, y của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình có cùng đơn vị đo là cm.
Vì AD là phân giác góc nên ta có:
=> x = 12cm => y = 28 – x = 16 cm
Vậy x = 12cm; y = 16cm
Đáp án: D
Câu 6:
Cho hình vẽ, biết rằng các số trên hình có cùng đơn vị đo. Tính giá trị biểu thức .
Vì AD là phân giác góc nên ta có:
Theo tính chất dãy tỉ số bằng nhau ta có:
=> BD = 3. = ; DC = 4.
Do đó x = , y =
Vậy S = 4100
Đáp án: C
Câu 7:
Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu đúng:
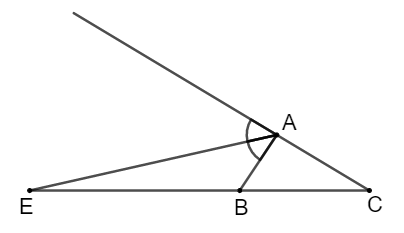
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên
Đáp án D
Câu 8:
Cho ΔABC, AE là phân giác ngoài của góc A. Hãy chọn câu sai:
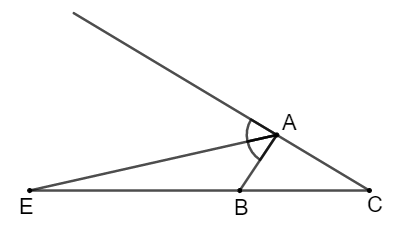
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thanh hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên
nên C đúng
nên A đúng
Chỉ có B sai.
Đáp án: B
Câu 9:
Cho ΔMNP, MA là phân giác ngoài của góc M, biết . Hãy chọn câu đúng:
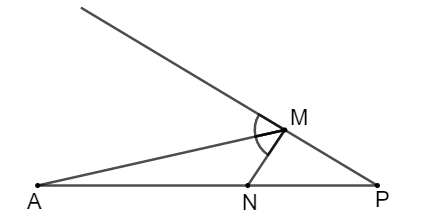
Theo tính chất đường phân giác của tam giác ta có
Đáp án: D
Câu 10:
Cho ΔMNP, MA là phân giác ngoài của góc M, biết . Hãy chọn câu sai:
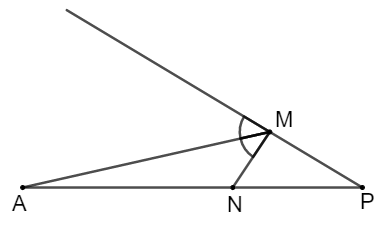
Theo tính chất đường phân giác của tam giác ta có: và MP = 3MN nên B, D đúng.
Ngoài ra: nên A đúng.
Chỉ có C sai.
Đáp án: C
Câu 11:
Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC, khi đó
Vì AD là phân giác của ΔABC nên:
Theo bài, ta có: AC = 2AB
Đáp án: D
Câu 12:
Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC. Xét các khẳng định sau, số khẳng định đúng là:
(I)
(II)
(III)
Vì AD là đường phân giác của tam giác ABC nên:
Theo bài, ta có: AC = 2AB hay (I) đúng
Lại có: nên (III) sai.
hay (II) đúng
Vậy chỉ có 2 khẳng định đúng.
Đáp án: D
Câu 13:
Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?
Vì BD là đường phân giác của nên:
Suy ra: (theo tính chất dãy tỉ số bằng nhau)
Mà tam giác ABC cân tại A nên AC = AB = 15cm
Đáp án: C
Câu 14:
Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là:
Tam giác ABC vuông tại A, áp dụng định lý Pytago có:
BD là tia phân giác góc B nên
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
=> DA= 3.1 = 3; DC = 5.1 = 5
Vậy AD = 3.
Đáp án: B
Câu 15:
Cho tam giác ABC, , AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của cắt HB tại D. Tia phân giác của cắt HC tại E. Tính DH?
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
Ta có: = .AB.AC = .AH.BC
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
Vì AD là phân giác của tam giác ABH nên:
ó 15DH = 108 – 12DH ó DH = 4cm
Đáp án: A
Câu 16:
Cho tam giác ABC, , AB = 15cm, AC = 20cm, đường cao AH (H Є BC). Tia phân giác của cắt HB tại D. Tia phân giác của cắt HC tại E. Tính HE?
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
Ta có: = .AB.AC = .AH.BC
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
Vì AE là phân giác của tam giác CAH nên:
ó ó 20HE = 12(16 – HE) ó 20HE + 12HE = 12.16
ó 32HE = 192 ó HE = 6(cm)
Đáp án: B
Câu 17:
Cho tam giác ABC, AB = AC = 10cm, BC = 12cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Tính BI?
Ta có: AB = AC = 10cm
Suy ra ΔABC cân tại A
Có I là giao các đường phân giác của ΔABC
Suy ra AI, BI là đường phân giác của ΔABC
Gọi H là giao của AI và BC
Khi đó ta có AH vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến ứng với cạnh đáy của tam giác cân ABC (tính chất tam giác cân).
=> H là trung điểm của cạnh BC
=> BH = HC = = 6cm
Áp dụng định lý Pitago trong tam giác ABH vuông tại H, ta có:
Vì BI là phân giác của tam giác ABH nên:
ó ó 10IH = 48 – 6IH ó IH = 3
Áp dụng định lý Pitago trong tam giác BHI vuông tại H, ta có:
Đáp án: D
