Dạng 1: Chứng minh tứ giác là hình chữ nhật có đáp án
-
968 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA
a) Chứng minh EFGH là hình bình hành.
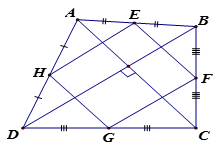
a) Ta có: là đường trung bình của và (1)
Ta có: là đường trung bình của và (2)
Từ (1), (2) suy ra EF // HG và EF = HG
Vậy EFGH là hình bình hành (3)
Câu 2:
b) Ta có: EFGH là hình bình hành.
Ta có: là đường trung bình của
Ta có:
Ta có: (4)
Từ (3), (4), suy ra hình bình hành EFGH có nên EFGH là hình chữ nhật.
Câu 3:
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với
a) Chứng minh PM = CQ.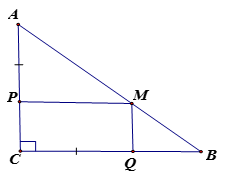
a) Ta có: ( vì vuông cân tại C ) (1)
Vì PM // BC nên ( hai góc đồng vị) (2)
Từ (1), (2) suy ra ( vì cùng bằng )
cân tại P => AP = PM ( hai cạnh bên bằng nhau)
Ta có:
Câu 4:
b) Ta có: là hình bình hành ( tứ giác có một cặp cạnh đối song song và bằng nhau)
Lại có
Vậy PCQM là hình chữ nhật.
Câu 5:
Cho tam giác ABC, các trung tuyến BM và CN cắt nhau tại G. Gọi P là điểm đối xứng của M qua G, gọi Q là điểm đối xứng của N qua G.
a) Tứ giác MNPQ là hình gì? Vì sao?
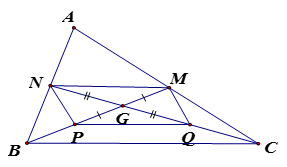
a) Ta có:
GM = GP (vì P là điểm đối xứng của M qua G) (1)
GN = GQ ( vì Q là điểm đối xứng của N qua G) (2)
Từ (1), (2) suy ra MNPQ là hình bình hành ( vì có G là trung điểm của hai đường chéo MP và NQ )
Câu 6:
b) Nếu cân tại A thì AB = AC, khi đó ta có
=> MB = NC vì thế ta lại có MP = NQ. Từ giác MNPQ là hình chữ nhật.
