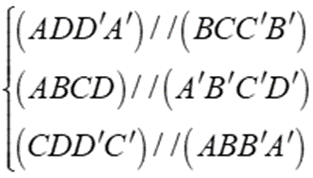Trắc nghiệm chuyên đề Toán 8 Chủ đề 1: Hình hộp chữ nhật có đáp án
-
1310 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
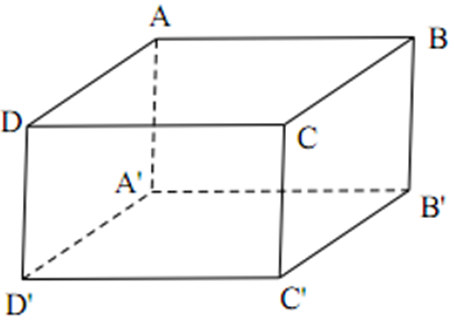
Cho hình hộp chữ nhật ABCD.A'B'C'D'
Nếu O là trung điểm của đoạn CB1 thì O có là điểm thuộc đoạn BC1 ? b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB1 hay không?
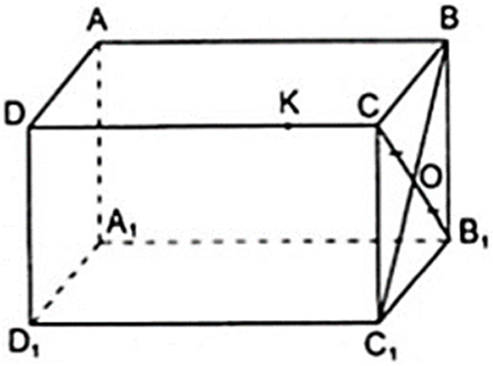
Câu trả lời trên là có. Thật vậy, vì mặt bên BCC1B1 là hình chữ nhật có O là trung điểm của đường chéo CB1 nên O cũng là trung điểm của đường chéo BC1 (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn BC1.
Câu 2:
Cho hình hộp chữ nhật ABCD.A'B'C'D'
K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB1 hay không?
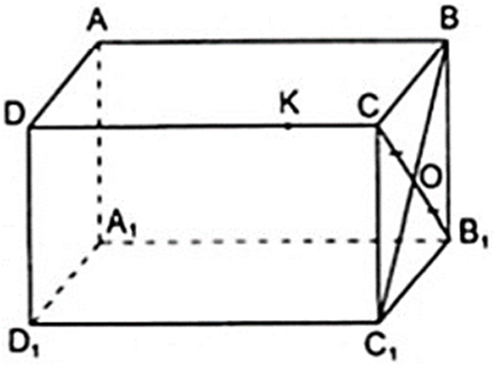
K không thuộc cạnh BB1 vì K ∉ mp( BB1C1C ) mà BB1 thuộc mặt phẳng đó
Vậy K không thuộc cạnh BB1.
Câu 3:
Các kích thước của hình hộp chữ nhật ABCD.A1B1C1D1 là DC = 5 cm; CB = 4cm; BB1 = 3 cm. Tính các độ dài DC1, CB1 ?
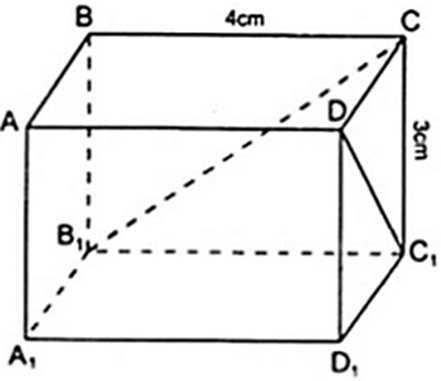
DC1 ∈ mp( DCC1D1 ) là hình chữ nhật nên Δ DCC1 vuông tại C.
Áp dụng định lý Py – ta – go vào Δ DCC1 vuông tại C ta được: DC12 = CC12 + CD2
Hay DC12 = 32 + 52 ⇔ DC12 = ( √ (34) )2 ⇔ DC1 = √ (34) ( cm )
CB1 ∈ ( BCC1B1 ) là hình chữ nhật nên Δ BCB1 vuông tại B.
Áp dụng định lí Py – ta – go vào Δ BCB1 vuông tại B ta được: CB12 = CB2 + BB12
Hay CB12 = 32 + 42 = 52 ⇔ CB1 = 5( cm )
Vậy DC1 = √ (34) ( cm ); CB1 = 5( cm )
Câu 4:
Số mặt, số đỉnh, số cạnh của hình lập phương là?
Hình lập phương cũng được gọi là hình hộp chữ nhật có 6 mặt, 8 đỉnh, 12 cạnh.
Chọn đáp án B.
Câu 5:
Hình hộp chữ nhật có số cặp mặt song song là?
Hình hộp chữ nhật có 3 cặp mặt song song.
Chọn đáp án B.
Câu 7:
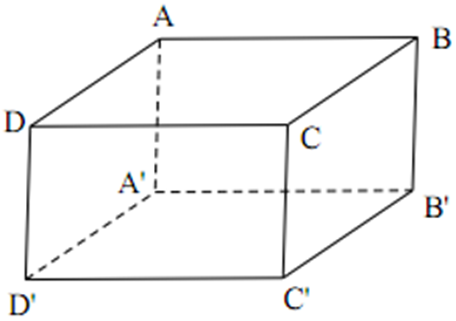
Ta có: ABCD là mặt đáy hình chữ nhật
⇒ AB//CD
Chọn đáp án A.
Câu 9:
Cho hình hộp chữ nhật ABCD.A'B'C'D'
a) Nếu O là trung điểm của đoạn CB1 thì O có là điểm thuộc đoạn BC1 ?
b) K là điểm thuộc cạnh CD, liệu K có thể là điểm thuộc cạnh BB1 hay không?
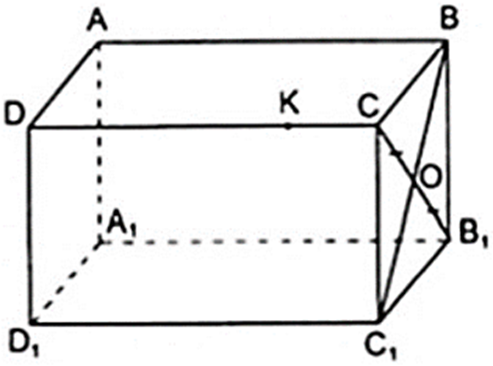
a) Câu trả lời trên là có. Thật vậy, vì mặt bên BCC1B1 là hình chữ nhật có O là trung điểm của đường chéo CB1 nên O cũng là trung điểm của đường chéo BC1 (theo tính chất đường chéo của hình chữ nhật). Vậy thuộc đoạn BC1.
b) K không thuộc cạnh BB1 vì K ∉ mp( BB1C1C ) mà BB1 thuộc mặt phẳng đó
Vậy K không thuộc cạnh BB1.
Câu 10:
Các kích thước của hình hộp chữ nhật ABCD.A1B1C1D1 là DC = 5 cm; CB = 4cm; BB1 = 3 cm. Tính các độ dài DC1, CB1 ?
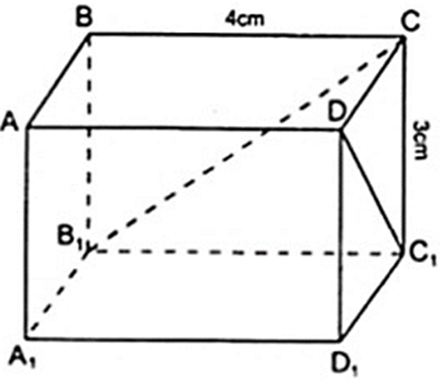
DC1 ∈ mp( DCC1D1 ) là hình chữ nhật nên Δ DCC1 vuông tại C.
Áp dụng định lý Py – ta – go vào Δ DCC1 vuông tại C ta được: DC12 = CC12 + CD2
Hay DC12 = 32 + 52 ⇔ DC12 = ( √ (34) )2 ⇔ DC1 = √ (34) ( cm )
CB1 ∈ ( BCC1B1 ) là hình chữ nhật nên Δ BCB1 vuông tại B.
Áp dụng định lí Py – ta – go vào Δ BCB1 vuông tại B ta được: CB12 = CB2 + BB12
Hay CB12 = 32 + 42 = 52 ⇔ CB1 = 5( cm )
Vậy DC1 = √ (34) ( cm ); CB1 = 5( cm )