Bài tập theo tuần Toán 8 - Tuần 3
-
363 lượt thi
-
19 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 17:
Cho hình tam giác ABC có M, N lần lượt là trung điểm của AB, AC . Biết BC = 10cm Tính MN
Xem đáp án
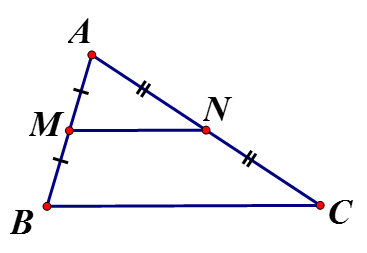

có M, N là trung điểm là đường trung bình
Vậy
Câu 18:
Cho sao cho . Gọi M là trung điểm BC, I là giao điểm của BD và AM. Chứng minh rằng AI = IM
Xem đáp án
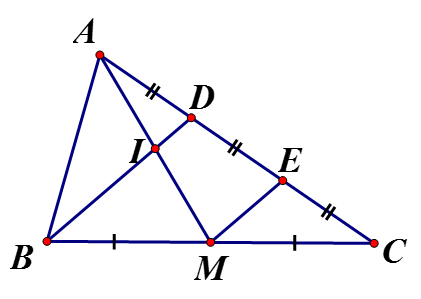

Gọi E là trung điểm
Xét có: M là trung điểm BC, E là trung điểm DC => ME là đường trung bình mà
Xét có D là trung điểm là trung điểm
VậyCâu 19:
Cho đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD, AC. Chứng minh rằng
Xem đáp án
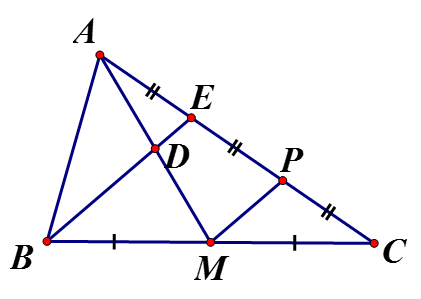

Vẽ MP//BE. Xét có: là trung điểm là trung điểm
Xét có D là trung điểm (do
=> E là trung điểm
Từ (1) và (2) suy ra