Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Bất phương trình bậc nhất một ẩn (Có đáp án)
Bài tập rèn luyện
-
283 lượt thi
-
18 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Ta có x - 3 < 4
⇔ x < 4 + 3 (chuyển vế - 3 và đổi dấu thành 3)
⇔ x < 7.
Vậy tập nghiệm của bất phương trình là { x| x < 7 }.
Câu 2:
Giải bất phương trình ≥ 2.
Ta có: ≥ 2
⇔ ≥ 2.3 (nhân cả hai vế với 3)
⇔ x - 1 ≥ 6 ⇔ x ≥ 7.
Vậy tập nghiệm của bất phương trình là { x| x ≥ 7 }.
Câu 3:
Giải bất phương trình ≤ - 1.
Ta có: 1 - ≤ - 1 ⇔ - ≤ - 2
⇔ -.( - 3 ) ≥ ( - 2 )( - 3 ) (nhân cả hai vế với - 3 và đổi dấu)
⇔ 2x ≥ 6 ⇔ x ≥ 3.
Vậy bất phương trình có tập nghiệm là { x| x ≥ 3 }.
Câu 4:
Giải bất phương trình 2x - 3 > 0
Ta có: 2x - 3 > 0
⇔ 2x > 3 (chuyển - 3 sang VP và đổi dấu)
⇔ 2x:2 > 3:2 (chia cả hai vế cho 2)
⇔ x > 3/2.
Vậy bất phương trình đã cho có tập nghiệm là { x| x > 3/2 }.
Câu 5:
Giải bất phương trình 2x - 1 ≤ 3x - 7
Ta có: 2x - 1 ≤ 3x - 7 ⇔ - 1 + 7 ≤ 3x - 2x
⇔ x ≥ 6.
Vậy bất phương trình đã cho có tập nghiệm là { x| x ≥ 6 }.
Câu 6:
Tìm tập nghiệm của các bất phương trình sau:
a) ( x + √ 3 )2 ≥ ( x - √ 3 )2 + 2
a) Ta có: ( x + √ 3 )2 ≥ ( x - √ 3 )2 + 2
⇔ x2 + 2√ 3 x + 3 ≥ x2 - 2√ 3 x + 3 + 2
⇔ 4√ 3 x ≥ 2 ⇔ x ≥ √ 3 /6 → S = [ √ 3 /6; + ∞ )
Vậy bất phương trình đã cho có tập nghiệm là S = [ √ 3 /6; + ∞ )
Câu 7:
b) x + √ x < ( 2√ x + 3 )( √ x - 1 )
b) Ta có: x + √ x < ( 2√ x + 3 )( √ x - 1 )
Điều kiện: x ≥ 0
⇔ x + √ x < 2x - 2√ x + 3√ x - 3
⇔ - x < - 3 ⇔ x > 3
Kết hợp điều kiện, tập nghiệm bất phương trình là: S = ( 3; + ∞ )
Vậy bất phương trình đã cho có tập nghiệm là S = ( 3; + ∞ )
Câu 8:
c) ( x - 3 )√ (x - 2) ≥ 2
c) Ta có: ( x - 3 )√ (x - 2) ≥ 2
Điều kiện: x ≥ 2
Bất phương trình tương đương là
Vậy tập nghiệm của bất phương trình là S = 2 ∪ [ 3; + ∞ )
Câu 9:
Có bao nhiêu giá trị thực của tham số m để bất phương trình ( m2 - m )x < m vô nghiệm là?
Rõ ràng nếu m2 - m ≠ 0 ⇔
thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.
Câu 10:
Bất phương trình ax + b > 0 vô nghiệm khi
Nếu a > 0 thì ax + b > 0 ⇔ x > - b/a nên
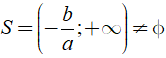
Nếu a < 0 thì ax + b > 0 ⇔ x < - b/a nên
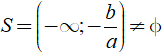
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Với b > 0 thì S = R.
Với b ≤ 0 thì S = Ø
Chọn đáp án D.
Câu 11:
Tập nghiệm S của bất phương trình: 5x - 1 ≥ + 3 là?
Ta có: 5x - 1 ≥ (2x)/5 + 3 ⇔ 25x - 5 ≥ 2x + 15 ⇔ 23x ≥ 20 ⇔ x ≥ 20/23.
Vậy tập nghiệm của bất phương trình là [ 20/23; + ∞ )
Chọn đáp án D.
Câu 12:
Bất phương trình có bao nhiêu nghiệm nguyên lớn hơn - 10 ?
Ta có:
⇔ 9x + 15 - 6 ≤ 2x + 4 + 6 ⇔ x ≤ - 5.
Vì x ∈ Z, - 10 < x ≤ - 5 nên có 5 nghiệm nguyên.
Chọn đáp án B.
Câu 13:
Tập nghiệm S của bất phương trình: ( 1 - √ 2 )x < 3 - 2√ 2 là?
Ta có: ( 1 - √ 2 )x < 3 - 2√ 2
Vậy tập nghiệm của bất phương trình là S = ( 1 - √ 2 ; + ∞ )
Chọn đáp án B.
Câu 14:
Bất phương trình ( 2x - 1 )( x + 3 ) - 3x + 1 ≤ ( x - 1 )( x + 3 ) + x2 - 5 có tập nghiệm là?
Ta có: ( 2x - 1 )( x + 3 ) - 3x + 1 ≤ ( x - 1 )( x + 3 ) + x2 - 5
⇔ 2x2 + 5x - 3 - 3x + 1 ≤ x2 + 2x - 3 + x2 - 5 ⇔ 0x ≤ - 6
⇔ x ∈ Ø → S = Ø
Chọn đáp án D.
Câu 15:
a) ( x + √ 3 )2 ≥ ( x - √ 3 )2 + 2
a) Ta có: ( x + √ 3 )2 ≥ ( x - √ 3 )2 + 2
⇔ x2 + 2√ 3 x + 3 ≥ x2 - 2√ 3 x + 3 + 2
⇔ 4√ 3 x ≥ 2 ⇔ x ≥ √ 3 /6 → S = [ √ 3 /6; + ∞ )
Vậy bất phương trình đã cho có tập nghiệm là S = [ √ 3 /6; + ∞ )
Câu 16:
b) x + √ x < ( 2√ x + 3 )( √ x - 1 )
b) Ta có: x + √ x < ( 2√ x + 3 )( √ x - 1 )
Điều kiện: x ≥ 0
⇔ x + √ x < 2x - 2√ x + 3√ x - 3
⇔ - x < - 3 ⇔ x > 3
Kết hợp điều kiện, tập nghiệm bất phương trình là: S = ( 3; + ∞ )
Vậy bất phương trình đã cho có tập nghiệm là S = ( 3; + ∞ )
Câu 17:
c) ( x - 3 )√ (x - 2) ≥ 2
c) Ta có: ( x - 3 )√ (x - 2) ≥ 2
Điều kiện: x ≥ 2
Bất phương trình tương đương là
Vậy tập nghiệm của bất phương trình là S = 2 ∪ [ 3; + ∞ )
Câu 18:
Có bao nhiêu giá trị thực của tham số m để bất phương trình ( m2 - m )x < m vô nghiệm là?
Rõ ràng nếu m2 - m ≠ 0 ⇔
thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.
