30 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 8 - Tuần 7

Câu 1:

Phân tích các đa thức sau thành nhân tử:

{(ab - 1)}^{2} + {(a + b)}^{2}

Xem đáp án

$\begin{array}{l} {(ab - 1)}^{2} + {(a + b)}^{2} \\ = a^{2} b^{2} - 2 ab + 1 + a^{2} + 2 ab + b^{2} \\ = a^{2} b^{2} + a^{2} + 1 + b^{2} = a^{2} (b^{2} + 1) + (b^{2} + 1) \\ = (a^{2} + 1) (b^{2} + 1) \end{array}$

Câu 2:

Phân tích đa thức sau thành nhân tử:

x^{3} + 2 x^{2} + 2 x + 1

Xem đáp án

$\begin{array}{l} x^{3} + 2 x^{2} + 2 x + 1 \\ = (x^{3} + 1) + (2 x^{2} + 2 x) \\ = (x + 1) (x^{2} - x + 1) + 2 x (x + 1) \\ = (x + 1) (x^{2} - x + 1 + 2 x) \\ = (x + 1) (x^{2} + x + 1) \end{array}$

Câu 3:

Phân tích đa thức sau thành nhân tử:

(1 + 2 x) (1 - 2 x) - x (x + 2) (x - 2)

Xem đáp án

$\begin{array}{l} (1 + 2 x) (1 - 2 x) - x (x + 2) (x - 2) \\ = 1 - 4 x^{2} - x (x^{2} - 4) \\ = - x^{3} - 4 x^{2} + 4 x + 1 \\ = - x^{3} + x^{2} - 5 x^{2} + 5 x - x + 1 \\ = - x^{2} (x - 1) - 5 x (x - 1) - (x - 1) \\ = (x - 1) (- x^{2} - 5 x - 1) = (x - 1) (x^{2} + 5 x + 1) \end{array}$

Câu 4:

Phân tích đa thức sau thành nhân tử:

x^{4} + 2 x^{3} - 4 x - 4

Xem đáp án

$\begin{array}{l} x^{4} + 2 x^{3} - 4 x - 4 \\ = x^{4} - 2 x^{2} + 2 x^{3} - 4 x + 2 x^{2} - 4 \\ = x^{2} (x^{2} - 2) + 2 x (x^{2} - 2) + 2 (x^{2} - 2) \\ = (x^{2} - 2) (x^{2} + 2 x + 2) \end{array}$

Câu 5:

Phân tích đa thức sau thành nhân tử:

x^{2} - 2 x - 4 y^{2} - 4 y

Xem đáp án

$\begin{array}{l} x^{2} - 2 x - 4 y^{2} - 4 y \\ = (x^{2} - 4 y^{2}) - 2 x - 4 y \\ = (x - 2 y) (x + 2 y) - 2 (x + 2 y) \\ = (x + 2 y) (x - 2 y - 2) \end{array}$

Câu 6:

Phân tích đa thức sau thành nhân tử:

x^{2} + y^{2} - x^{2} y^{2} + xy - x - y

Xem đáp án

$\begin{array}{l} x^{2} + y^{2} - x^{2} y^{2} + xy - x - y \\ = x^{2} - x^{2} y^{2} + y^{2} - y + xy - x \\ = - x^{2} (y^{2} - 1) + y (y - 1) + x (y - 1) \\ = (y - 1) [- x^{2} (y + 1) + y + x] \\ = (y - 1) . (- x^{2} y - x^{2} + y + x) \\ = (y - 1) [(y - x^{2} y) - (x^{2} - x)] \\ = (y - 1) [- y (x^{2} - 1) - x (x - 1)] \\ = (y - 1) [(x - 1) (- y (x + 1) - x)] \\ = (y - 1) (x - 1) (- xy - y - x) \end{array}$

Câu 7:

Phân tích đa thức sau thành nhân tử:

x^{2} + 2 xy + y^{2} - x - y - 12

Xem đáp án

$\begin{array}{l} x^{2} + 2 xy + y^{2} - x - y - 12 \\ = {(x + y)}^{2} - (x + y) - 12 \\ = {(x + y)}^{2} - 4 (x + y) + 3 (x + y) - 12 \\ = (x + y) (x + y - 4) + 3 (x + y - 4) \\ = (x + y - 4) (x + y + 3) \end{array}$

Câu 8:

Phân tích đa thức sau thành nhân tử:

16 x - 5 x^{2} - 3

Xem đáp án

$\begin{array}{l} 16 x - 5 x^{2} - 3 \\ = - 5 x^{2} + x + 15 x - 3 \\ = x (1 - 5 x) - 3 (1 - 5 x) \\ = (x - 3) (1 - 5 x) \end{array}$

Câu 9:

Phân tích đa thức sau thành nhân tử:

x^{2} - 4 x - 5

Xem đáp án

$\begin{array}{l} x^{2} - 4 x - 5 \\ = x^{2} + x - 5 x - 5 \\ = x (x + 1) - 5 (x + 1) \\ = (x + 1) (x - 5) \end{array}$

Câu 10:

Phân tích đa thức sau thành nhân tử:

3 x^{2} - 6 xy + 3 y^{2} - 12 z^{2}

Xem đáp án

$\begin{array}{l} 3 x^{2} - 6 xy + 3 y^{2} - 12 z^{2} \\ = 3 (x^{2} - 2 xy + y^{2} - 4 z^{2}) \\ = 3 [{(x - y)}^{2} - {(2 z)}^{2}] \\ = 3 (x - y - 2 z) (x - y + 2 z) \end{array}$

Câu 11:

Phân tích đa thức sau thành nhân tử:

x^{3} - 7 x - 6

Xem đáp án

$\begin{array}{l} x^{3} - 7 x - 6 \\ = x^{3} - x - 6 x - 6 \\ = x (x^{2} - 1) - 6 (x + 1) \\ = x (x - 1) (x + 1) - 6 (x + 1) \\ = (x + 1) [x (x - 1) - 6] \\ = (x + 1) (x^{2} - x - 6) \\ = (x + 1) (x^{2} - 3 x + 2 x - 6) \\ = (x + 1) [x (x - 3) + 2 (x - 3)] \\ = (x + 1) (x - 3) (x + 2) \end{array}$

Câu 12:

Phân tích đa thức sau thành nhân tử:

5 x^{2} - 10 xy + 5 y^{2} - 20 z^{2}

Xem đáp án

$\begin{array}{l} 5 x^{2} - 10 xy + 5 y^{2} - 20 z^{2} \\ = 5 (x^{2} - 2 xy + y^{2} - 4 z^{2}) \\ = 5 [{(x - y)}^{2} - {(2 z)}^{2}] \\ = 5 (x - y - 2 z) (x - y + 2 z) \end{array}$

Câu 13:

Phân tích đa thức sau thành nhân tử:

x^{2} - 5 x + 5 y - y^{2}

Xem đáp án

$\begin{array}{l} x^{2} - 5 x + 5 y - y^{2} \\ = (x^{2} - y^{2}) - (5 x - 5 y) \\ = (x - y) (x + y) - 5 (x - y) \\ = (x - y) (x + y - 5) \end{array}$

Câu 14:

Phân tích đa thức sau thành nhân tử:

{(x^{2} + 1)}^{2} - 4 x^{2}

Xem đáp án

$\begin{array}{l} {(x^{2} + 1)}^{2} - 4 x^{2} \\ = {(x^{2} + 1)}^{2} - {(2 x)}^{2} \\ = (x^{2} + 2 x + 1) (x^{2} - 2 x + 1) \\ = {(x + 1)}^{2} . {(x - 1)}^{2} \end{array}$

Câu 15:

Tìm x, biết: $3 x (x - 2) - x + 2 = 0$

Xem đáp án

$\begin{array}{l} 3 x (x - 2) - x + 2 = 0 \\ 3 x (x - 2) - (x - 2) = 0 \\ (x - 2) (3 x - 1) = 0 \\ \Rightarrow [\begin{array}{l} x - 2 = 0 \\ 3 x - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = \frac{1}{3} \end{array} \end{array}$

Câu 16:

Tìm x biết: $4 x (x - 3) - 2 x + 6 = 0$

Xem đáp án

$\begin{array}{l} 4 x (x - 3) - 2 x + 6 = 0 \\ 4 x (x - 3) - 2 (x - 3) = 0 \\ (x - 3) (4 x - 2) = 0 \\ \Rightarrow [\begin{array}{l} x - 3 = 0 \\ 4 x - 2 = 0 \end{array} \Rightarrow [\begin{array}{l} x = 3 \\ x = \frac{1}{2} \end{array} \end{array}$

Câu 17:

Tìm x biết: $2 x (x - 4) + x - 4 = 0$

Xem đáp án

$\begin{array}{l} 2 x (x - 4) + x - 4 = 0 \\ (x - 4) (2 x + 1) = 0 \\ \Rightarrow [\begin{array}{l} x = 4 \\ x = - \frac{1}{2} \end{array} \end{array}$

Câu 18:

Tìm x biết: $2 x^{3} + 4 x = 0$

Xem đáp án

$\begin{array}{l} 2 x^{3} + 4 x = 0 \Rightarrow 2 x (x^{2} + 2) = 0 \\ \Rightarrow 2 x = 0 (do x^{2} + 2 > 0) \\ \Leftrightarrow x = 0 \end{array}$

Câu 19:

Tính nhanh: $101^{2}$

Xem đáp án

$\begin{array}{l} 101^{2} = {(100 + 1)}^{2} = 100^{2} + 2 .100.1 + 1 \\ = 10000 + 200 + 1 = 10201 \end{array}$

Câu 20:

Tính nhanh: $97 .103$

Xem đáp án

$\begin{array}{l} 97 .103 = (100 - 3) (100 + 3) \\ = 100^{2} - 3^{2} = 10000 - 9 = 9991 \end{array}$

Câu 21:

Tính nhanh: $77^{2} + 23^{2} + 77 .46$

Xem đáp án

$\begin{array}{l} 77^{2} + 23^{2} + 77 .46 \\ = 77^{2} + 2 .77.23 + 23^{2} \\ = {(77 + 23)}^{2} = 100^{2} = 10 000 \end{array}$

Câu 22:

Tính nhanh:

105^{2} - 5^{2}

Xem đáp án

$\begin{array}{l} 105^{2} - 5^{2} = (105 - 5) (105 + 5) \\ = 100.110 = 10 = 1 1 000 \end{array}$

Câu 23:

Tính nhanh:

85^{2} + 15^{2} + 85.30

Xem đáp án

$\begin{array}{l} 85^{2} + 15^{2} + 85.30 \\ = 85^{2} + 2.15.85 + 15^{2} \\ = {(85 + 15)}^{2} = 100^{2} = 10000 \end{array}$

Câu 24:

Tính nhanh: $106^{2} - 36$

Xem đáp án

$\begin{array}{l} 106^{2} - 36 = 106^{2} - 6^{2} \\ = (106 - 6) (106 + 6) \\ = 112.100 = 11200 \end{array}$

Câu 25:

Thực hiện phép tính:

{(6 x + 1)}^{2} + {(6 x - 1)}^{2} - 2 (1 + 6 x) (6 x - 1)

Xem đáp án

$\begin{array}{l} {(6 x + 1)}^{2} + {(6 x - 1)}^{2} - 2 (1 + 6 x) (6 x - 1) \\ = {(6 x + 1)}^{2} - 2 . (6 x + 1) (6 x - 1) + {(6 x - 1)}^{2} \\ = {(6 x + 1 - 6 x + 1)}^{2} = 2^{2} = 4 \end{array}$

Câu 26:

Thực hiện phép tính:

3 x (x - 2) - 5 x (1 - x) - 8 (x^{2} - 3)

Xem đáp án

$\begin{array}{l} 3 x (x - 2) - 5 x (1 - x) - 8 (x^{2} - 3) \\ = 3 x^{2} - 6 x - 5 x + 5 x^{2} - 8 x^{2} + 24 \\ = - 11 x + 24 \end{array}$

Câu 27:

Thực hiện phép tính:

(x^{2} - 1) (x^{2} + 2 x)

Xem đáp án

$(x^{2} - 1) (x^{2} + 2 x) = x^{4} + 2 x^{3} - x^{2} - 2 x$

Câu 28:

Cho hình bình hành ABCD gọi O là giao điểm hai đường chéo. Qua O vẽ đường thẳng cắt hai cạnh AB, CD ở E, F. Qua O vẽ đường thẳng cắt 2 cạnh AD, BC ở G và H. Chứng minh EFGH là hình bình hành.

Xem đáp án

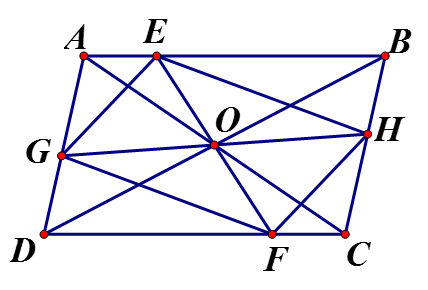
Cho hình bình hành ABCD gọi O là giao điểm hai đường chéo. Qua O vẽ đường thẳng cắt hai cạnh AB, CD ở E, F. (ảnh 1)

Xét $Δ A E O$ và $Δ C F O$ có:

$\hat{A O E} = \hat{C O F}$ (đối đỉnh); $O A = O C (g t); \hat{E A O} = \hat{F C O}$ (so le trong)

$\Rightarrow Δ A E O = Δ C F O (g . c . g) \Rightarrow O E = O F (1)$

Chứng minh tương tự ta có: $Δ G A O = Δ H C O (g . c . g) \Rightarrow O G = O H (2)$

Từ (1) và (2) suy ra tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm O mỗi đường nên là EFGH hình bình hành.

Câu 29:

Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M . Tính số đo các góc:

\hat{A B K}; \hat{A C K}

Xem đáp án

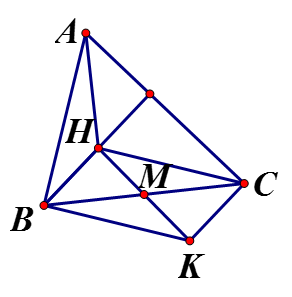
Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M . Tính số đo các góc: (ảnh 1)

Tứ giác BHCK có hai đường chéo BC, HK cắt nhau tại trung điểm mỗi đường nên BHCK là hình bình hành nên $\{\begin{cases} B H / / C K \\ B K / / C H \end{cases}$

Ta có: $B H ⊥ A C$ (vì H là trực tâm) mà $B H / / C K \Rightarrow K C ⊥ A C$

$C m t t \Rightarrow \hat{A B K} = 90^{0}$

Câu 30:

Cho hình bình hành ABCD, O là giao điểm 2 đường chéo AC và BD. Gọi E là một điểm thuộc cạnh AB, F là giao điểm của EO và CD. Vẽ

F H / / A C, E G / / A C (H \in A D, G \in B C) .

Chứng minh rằng: điểm H đối xứng với G qua O.

Xem đáp án

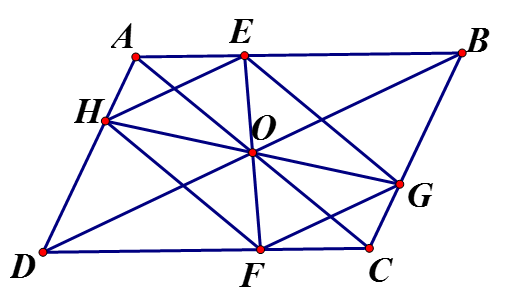
Cho hình bình hành ABCD, O là giao điểm 2 đường chéo AC và BD. Gọi E là một điểm thuộc cạnh AB, F là giao điểm của EO và CD. (ảnh 1)

$Δ O E B$ và $Δ O F D$ có: $\hat{E O B} = \hat{F O D}$ (đối đỉnh); $O B = O D$ (tính chất hình bình hành)

$\hat{E B O} = \hat{F D O}$ (so le trong) $\Rightarrow Δ O E B = Δ O F D (g . c . g) \Rightarrow B E = F D$

Ta có: $E G / / F H$ (cùng // AC), do đó

$\hat{B E G} = \hat{D F H}, E B = F H (c m t); \hat{B} = \hat{D}$ (tính chất hình bình hành)

$\Rightarrow Δ B E G = Δ D F C (g . c . g) \Rightarrow E G = F H$

Tứ giác EGFH có $\{\begin{cases} E G / / F H \\ E G = F H \end{cases}$ nên là hình bình hành

Do đó O là trung điểm HG. nên H và G đối xứng nhau qua O.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 8 - Tuần 7

Bài tập theo tuần Toán 8 - Tuần 7

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương