Dạng 1. Vận dụng tính chất của hình bình hành để chứng minh các tính chất hình học có đáp án
-
702 lượt thi
-
4 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD .
a) Chứng minh rằng AF // CE .
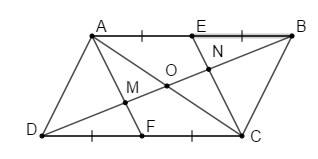
a) Ta có ABCD là hình bình hành nên
AB = CD (tc hbh).
Mà E, F là trung điểm cuả AB và CD
=> AB = CF = BE = DF .
Xét tứ giác AECF, có
AEFC là hình bình hành => AF // ECCâu 2:
Xét có DO, AF là trung tuyến;
=> M là trọng tâm của
Xét có: BO, CE là trung tuyến,
=> N là trọng tâm của
Từ (2) và (4)
Từ (1); (3) và (5)
=> DM = BN = MN (đpcm).Câu 3:
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo, E và F theo thứ tự là trung điểm của OD và OB
a) Chứng minh rằng AE // CF
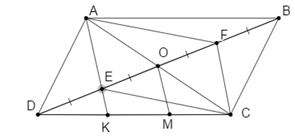
a)
E, F là trung điểm của DO và BO nên: DE = EO = OF = FB
Xét tứ giác AFCE, có:
=> AFCE là hình bình hành (dhnb)
=> AE // CF (tc hbh).Câu 4:
Xét có OM // EK và E là trung điểm của DO
=> K là trung điểm của DM
=> DK = KM (1)
Xét , có OM // AK và O là trung điểm của AC
=> M là trung điểm của KC
=> CM = KM (2)
Từ (1) và (2) => DK = KM = CM
Mà KM + CM = KC
(đpcm).
