Bài tập Toán 8 Chủ đề 5: Đường trung bình của tam giác, của hình thang có đáp án
Dạng 1. Sử dụng định nghĩa và định lí về đường trung bìn của tam giác để chứng minh có đáp án
-
694 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:
a) EF là đường trung bình của tam giác ABC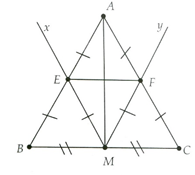
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
Câu 2:
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.
Câu 3:
Cho tam giác ABC, có AM là trung tuyến ứng với BC. Trên cạnh AB lấy điểm D và E sao cho AD = DE = EB. Đoạn CD cắt AM tại I. Chứng minh:
a) EM song song vói DC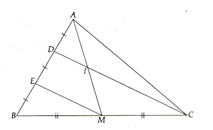
a) Ta có EM là đường trung bình của tam giác BCD => ĐPCM.
Câu 4:
Câu 5:
c) Vì DI là đường trung bình của tam giác AEM nên DI = EM.(1)
Tương tự, ta được: EM = DC (2)
Từ (1) và (2) Þ DC = 4DI
Câu 6:
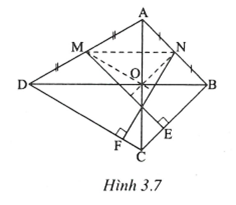
Gọi O là giao điểm của AC và BD.
Ta có: và OA = OC.
Xét có MN là đường trung bình
=> MN // BD và (vì ).
Xét có ON là đường trung bình
=> ON // BC và (vì ).
Xét có OM là đường trung bình
=> OM // CDvà (vì ).
Xét có OA, ME, NF là ba đường cao nên chúng đồng quy.
Câu 7:
Cho tam giác ABC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E. Gọi M, N lần lượt là trung điểm của BE và CD. Đường thẳng MN cắt tia AB và AC lần lượt là tại P và Q. Hỏi hai điểm D và E phải có điều kiện gì để tam giác APQ cân tại A?
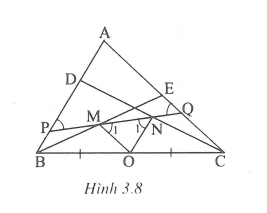
Gọi O là trung điểm của BC.
Xét có OMlà đường trung bình
=> OM // CE và .
Xét có ON là đường trung bình
=> ON // BD và .
Ta có: (so le trong).
cân tại .
Câu 8:
Cho tam giác ABC. Gọi Bx và Cy lần lượt là các đường chứa tia phân giác của các góc ngoài tại đỉnh B và C. Gọi H và K lần lượt là hình chiếu của A trên Bx và Cy.
a) Chứng minh rằng tứ giác BCKH là hình thang;
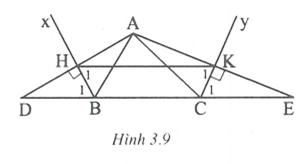
a) Gọi D và E thứ tự là giao điểm của AH và AK với đường thẳng BC.
có BH vừa là đường phân giác, vừa là đường cao nên là tam giác cân => HA = HD.
Tương tự, ta có: KA = KE.
Xét có HK là đường trung
bình nên HK // DE
=> HK // BCDo đó tứ giác BCKH là hình thang.
Câu 9:
b) Ta có: (so le trong).
Hình thang BCKH là hình thang cân
cân tại ![]() .
.
Câu 10:
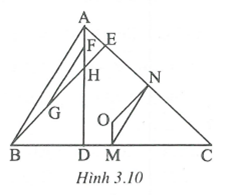
Gọi M và N lần lượt là trung điểm của BC và CA.
Gọi F và G lần lượt là trung điểm của AH và BG.
Ta có MN là đường trung bình của , FG là đường trung bình của .
Suy ra MN // AB và
FG = AB và .
Do đó MN // FG và MN = FG. Dễ thấy .
và có: (hai góc có cạnh tương ứng song song).
Vậy .
Câu 11:
Cho tam giác ABCcân tại A, đường cao AH và đường phân giác BD. Biết rằng , tính số đo các góc của tam giác ABC
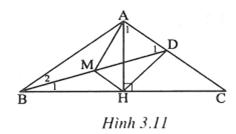
Gọi M là trung điểm của BD thì: .
cân tại A, AH là đường cao nên HB = HC.
Ta có HM là đường trung bình của .
Hình thang HMAD có hai đường chéo bằng nhau nên là hình thang cân.
(1)
Ta đặt thì
Vậy có .
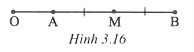
Câu 12:
Gọi M là trung điểm của AB và O là một điểm tùy ý không nằm giữa A và B.
- Trường hợp O nằm trên tia đối của tia AB hay tia đối của tia BA (h.3.16), ta chứng minh được
- Trường hợp O không thẳng hàng với A và B (h.3.17).
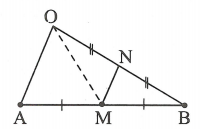
Gọi N là trung điểm của OB, khi đó MN là đường trung bình của .
Xét , ta có:
Từ (1) và (2) suy ra:
Áp dụng hệ thức (*) đối với n điểm ta có:
Cộng từng vế các bất đẳng thức trên ta được:
Như vậy điểm cần tìm chính là trung điểm M của AB.
