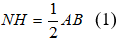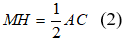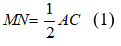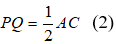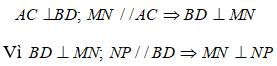Bài tập Hình vuông (có lời giải chi tiết)
-
886 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hãy khoanh tròn vào phương án đúng nhất trong các phương án sau ?
+ Tứ giác có 4 góc vuông là hình chữ nhật
Hình chữ nhật có 4 cạnh bằng nhau là hình vuông.
⇒ Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
Chọn đáp án A.
Câu 2:
Hãy chọn đáp án sai trong các phương án sau đây ?
+ Trong hình vuông có hai đường chéo vuông góc với nhau, bằng nhau và cắt nhau tại trung điểm mỗi đường
+ Hai đường chéo trong hình vuông đồng thời là trục đối xứng của hình vuông đó.
→ Đáp án B sai.
Chọn đáp án B.
Câu 3:
Trong các dấu hiệu nhận biết sau thì dấu hiệu nào không đủ điều kiện để tứ giác là hình vuông?
Dấu hiệu nhận biết hình vuông:
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
→ Hình bình hành có hai đường chéo bằng nhau thì không là hình vuông.
→ Đáp án D sai.
Chọn đáp án D.
Câu 4:
Tìm câu nói đúng khi nói về hình vuông?
Dấu hiệu nhận biết hình vuông:
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
⇒ Hình vuông vừa là hình chữ nhật, cũng vừa là hình thoi.
⇒ Cả 3 phương án đều đúng.
Chọn đáp án D.
Câu 5:
Một hình vuông có độ dài cạnh bằng 4cm thì độ dài đường chéo của hình vuông là ?
Hình vuông có độ dài cạnh là a (cm) (a > 0)
Áp dụng định lý Py – ta – go thì độ dài đường chéo của hình vuông là ( cm )
Do đó với a = 4 thì độ dài đường chéo là
Chọn đáp án B.
Câu 6:
Hình bình hành có 1 góc vuông là:
Hình bình hành có 1 góc vuông là hình chữ nhật
Chọn đáp án B
Câu 9:
Cho tam giác ABC vuông cân tại A có M; N và H lần lượt là trung điểm của AB; AC và BC. Hỏi tứ giác AMHN là hình gì ? Chọn câu trả lời đúng nhất
* Vì N và H lần lượt là trung điểm của AC và BC nên NH là đường trung bình của tam giác ABC
Suy ra: NH // AB và
* Chứng minh tương tự, có MH là đường trung bình của tam giác ABC nên:
MH // AC và
Do đó: AM // NH và AN // MH
* Tứ giác AMHN có 2 các cạnh đối song song với nhau nên là hình bình hành
Lại có : nên tứ giác AMHN là hình chữ nhật.
* Theo giả thiết, tam giác ABC là tam giác vuông cân tại A nên AC = AB (3)
Từ (1); (2) và (3) suy ra: NH = MH.
Hình chữ nhật AMHN có hai cạnh liền kề NH và MH bằng nhau nên là hình vuông
Chọn đáp án A
Câu 10:
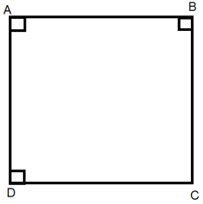
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q theo thứ tự là trung điểm của AB; BC; CD và DA. Hỏi tứ giác MNPQ là hình gì
* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác
Suy ra: MN// AC và
* Xét tam giác ACD có P và Q lần lượt là trung điểm của CD và AD nên PQ là đường trung bình của tam giác
Suy ra: PQ // AC và
Từ (1) và (2) suy ra: MN// PQ và MN = PQ
Do đó, tứ giác MNPQ là hình bình hành.
* Xét tam giác BCD có P và N lần lượt là trung điểm của CD và CB nên PN là đường trung bình của tam giác
Suy ra: NP // BD
* Ta có
Hình bình hành MNPQ có 1 góc vuông nên là hình chữ nhật.
Vì hai cạnh kề của hình chữ nhật MNPQ chưa chắc đã bằng nhau (không có dữ kiện liên quan) nên MNPQ không thể là hình vuông.
Chọn đáp án C