Dạng 1. Vẽ tam giác đồng dạng với tam giác cho trước.Chứng minh hai tam giác đồng dạng
-
446 lượt thi
-
5 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giả sử đã vẽ được theo tỉ số , thế thì .
Từ đó suy ra cách vẽ gồm hai bước sau:
Bước 1: Trên cạnh AB lấy điểm M sao cho .
Bước 2: Kẻ cắt AC ở N.
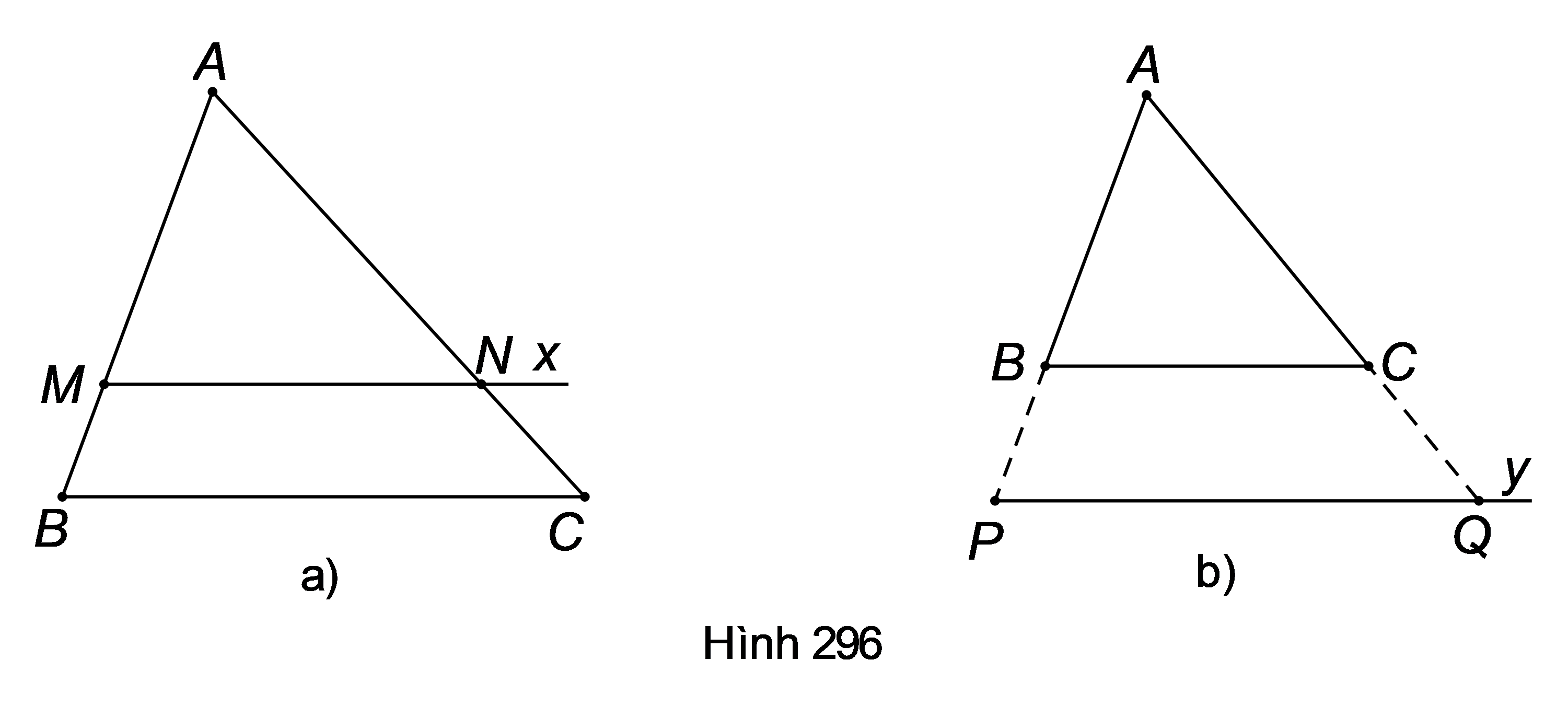
Ta có theo tỉ số .
Câu 2:

Giả sử đã vẽ được theo tỉ số thế thì .
Từ đó suy ra cách vẽ gồm hai bước sau:
Bước 1: Trên tia AB lấy điểm P sao cho .
Bước 2: Kẻ cắt tia AC ở Q. Ta có .
Câu 3:
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = 2AB. Trên tia đối của tia AC lấy điểm E sao cho AE = 2AC. Chứng minh ADE đồng dạng với ABC.
Lấy M, N lần lượt là trung điểm của AD, AE.
Từ đó chứng minh được
∆AMN ∆ADE (định lí)
∆ABC ∆AMN (do hai tam giác bằng nhau)
⇒ ∆ABC ∆ADE
Câu 4:
Từ điểm D trên cạnh AB của tam giác ABC, kẻ một đường thằng song song với AB tại F; BF cắt AC ở I. Tìm cặp tam giác đồng dạng.
Dùng định nghĩa để chứng minh:
∆ADE ∆CFE; ∆EFI ∆CBI; ∆FIC ∆BIA
⇒∆ABC ∆CFE (theo tính chất bắc cầu)
Câu 5:
Cho hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC. Chứng minh ba tam giác EDA, ABE, CEB đồng dạng với nhau.
Sử dụng tính chất các tam giác bằng nhau thì đồng dạng với nhau để chứng minh.
