Đề kiểm tra 45 phút Toán 8 Chương 3 Hình Học có đáp án (Đề 1)
-
2930 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Hai tam giác bằng nhau thì đồng dạng với nhau.....
b) Hai tam giác đồng dạng với nhau thì bằng nhau.....
a) Đúng b) Sai
Câu 3:
Biết tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số đồng dạng k = 4/5 . Khi đó tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng là:
Chọn A
Câu 4:
Cho tam giác ABC. Lấy D, E trên các cạnh AB, AC sao cho DE // BC và Độ dài cạnh AC là:
Chọn D
Câu 5:
Hai tam giác đồng dạng có tỉ số chu vi là 3/4 . Tỉ số diện tích tương ứng của hai tam giác đó là:
Chọn B
Câu 6:
Cho ΔABC vuông tại A. Đường cao AH chia cạnh huyền thành hai đoạn có độ dài 9cm và 16cm. Diện tích tam giác vuông đó là:
Chọn C
Câu 7:
Phần tự luận (7 điểm)
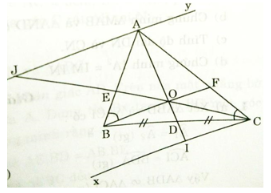
Cho tam giác ABC, trung tuyến AD, biết AB = 4cm; AC = 8cm. Qua B dựng đường thẳng cắt AC tại F sao cho góc ABF bằng góc ACB.
a) Chứng tỏ tam giác ABF và tam giác ACB đồng dạng. Tính độ dài đoạn CF
b) Chứng tỏ diện tích tam giác ABC bằng hai lần diện tích tam giác ADC
c) Gọi O là giao điểm của BF và AD, CO cắt AB tại E. Từ A và C lần lượt dựng các đường thẳng song song với BF cắt CO tại J và cắt AD tại I.
+ Chứng tỏ
+ Chứng tỏ
a) Xét ΔABF và ΔABC có :
∠A chung
∠ABF = ∠ACB (gt)
⇒ ΔABF ∼ ΔACB (g.g)
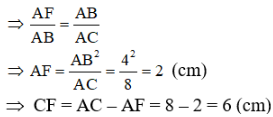
b) Ta có DB = DC (AD là trung tuyến của ΔABC)
![]() (Chung đường cao kẻ từ A và đáy DB = DC)
(Chung đường cao kẻ từ A và đáy DB = DC)
mà ![]()
![]()
c) Ta có Cx // BF (gt). Theo định lí Talét :
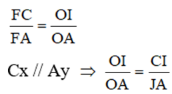
![]()
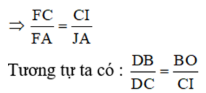
![]()
![]()
Mặt khác Ay//FB ta có:
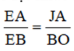
![]()
Câu 8:
Cho tam giác ABC. Trên cạnh AB lấy điểm P, trên cạnh AC lấy điểm Q sao cho Đường trung tuyến AM của ΔABC cắt PQ tại K. Chứng minh KP = KQ.
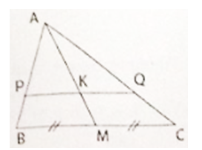
Ta có:
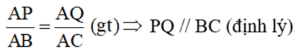
Vì K ∈ PQ nên PK // BM; KQ // MC
Trong ΔABM có PK // BM nên
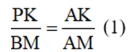
Trong ΔAMC có KQ // MC nên
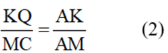
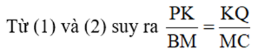
mà BM = MC (gt) nên PK = KQ.
