Trắc nghiệm chuyên đề Toán 8 Chủ đề 6. Ôn tập và kiểm tra có đáp án (Đề kiểm tra 1 tiết - Đề 1)
-
413 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Điền vào chỗ trống (…) để được khẳng định đúng.
Đa giác có tất cả các cạnh bằng nhau và tất cả các góc là ………Câu 4:
Đáp án A
Câu 5:
Cho hình vuông ABCD có cạnh 12cm (hình bên), AE = xcm,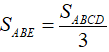 
. Độ dài của x là:
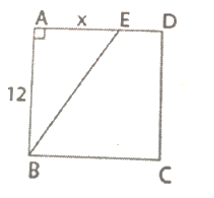
Đáp án D
Câu 6:
Đáp án B
Câu 7:
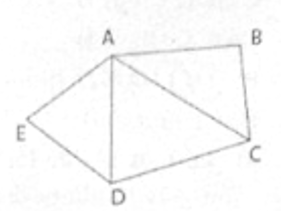
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 180o.
Tổng các góc trong của ngũ giác ABCDE là 180o.3 = 540o
Câu 8:
b) Vì ABCDE là ngũ giác đều nên
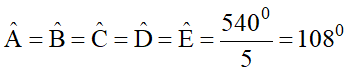
Mặt khác, ΔABC cân tại B nên:
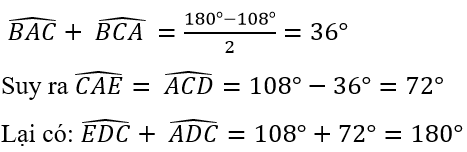
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt) nên tứ giác CEFD là hình thoi.
Câu 9:
Cho hình bình hành ABCD có diện tích S. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Đường thẳng BQ cắt AP tại E và cắt MC tại F. Đường thẳng DN cắt AP tại S và cắt MC tại R.
a) Chứng minh tứ giác EFRS là hình bình hành.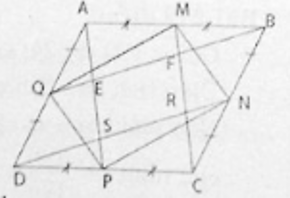
a) Ta có AB // CD (gt)
Suy ra AM // CP (1)
Lại có AM = AB/2; CP = CD/2 (2)
Từ (1) và (2) suy ra AMCP là hình bình hành
Suy ra AP // CM hay ES // FR.
Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.
Vậy tứ giác EFRS là hình bình hành
Câu 10:
b) Tính diện tích hình bình hành EFRS theo S.
b) Đặt PS = x. Suy ra CR = 2x (tính chất đường trung bình)
Từ đó suy ra RF = ES = AE = 2x
Suy ra: ES = 2. => SEFRS = 2.
Vì SAMCP = nên SEFRS =