Bài tập theo tuần Toán 8 - Tuần 13 (đề 2)
-
582 lượt thi
-
9 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 7:
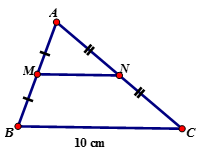
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Gọi I là trung điểm của BC. Tính độ dài đoạn thẳng IA
Xem đáp án
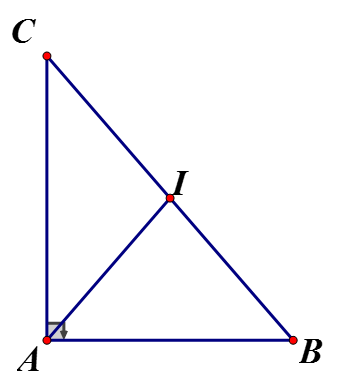

vuông tại A, theo định lý Pytago ta có :
Hay
vuông tại A, có AI là đường trung tuyếnCâu 8:
Cho tam giác ABC vuông tại A, gọi K là trung điểm BC, H là điểm đối xứng với A qua K. Tứ giác ACHB là hình gì? Vì sao?
Xem đáp án
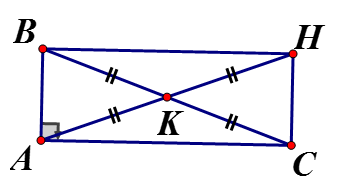

Tứ giác ACHB có hai đường chéo BC, AH cắt nhau tại trung điểm K mỗi đường
là hình bình hành mà là hình chữ nhậtCâu 9:
Cho tứ giác EFGH. Gọi A, B, C, D lần lượt là trung điểm của FH, EF, EG, GH.
a) Chứng minh tứ giác ABCD là hình bình hành
b) Tìm điều kiện của tứ giác EFGH để ABCD là hình thoi (Vẽ hình)
Xem đáp án
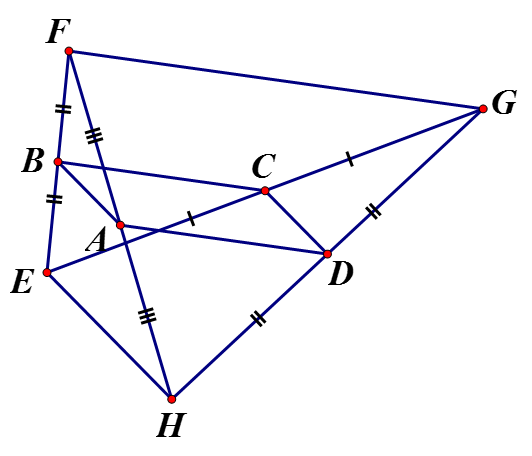

a) Xét có: A là trung điểm FH, D là trung điểm HG
là đường trung bình
Xét có B là trung điểm EF, C là trung điểm EG nên BC là đường trung bình
Từ (1) và (2) suy ra là hình bình hành.b) ABCD là hình thoi
Chứng minh tương tự câu a => CD là đường trung bình
Từ (1), (3), (4)
Vậy khi tứ giác EFGH có FG = EH thì ABCD là hình thoi.