Bài tập theo tuần Toán 8 - Tuần 8
-
324 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 9:
Tìm n để đa thức chia hết cho
Khi thực hiện phép chia ta có: Thương là và dư là
Để thì dư bằng 0
Câu 10:
Để thì
Câu 11:
Xác định các hằng số a và b sao cho: chia hết cho
Sau khi thực hiện phép chia ta được dư là
Để
Vậy thì thoả đề.
Câu 12:
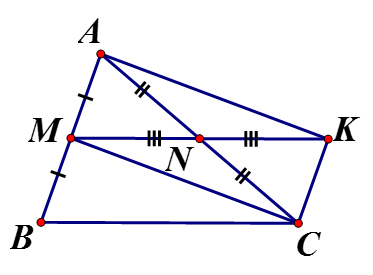
a) có: M là trung điểm AB, N là trung điểm AC
b) Ta có: (tính chất đường trung bình) mà
Vì đối xứng qua N nên
Từ (1) và (2) suy ra
Từ (a) và (b) suy ra BMKC là hình bình hànhc) Tứ giác AKCM có hai đường chéo AC, MK cắt nhau tại trung điểm N mỗi đường nên AKCM là hình bình hành
d) BMKC là hình chữ nhật mà M là trung điểm vừa là đường cao, vừa là đường trung tuyến trong cân tại C
Câu 13:
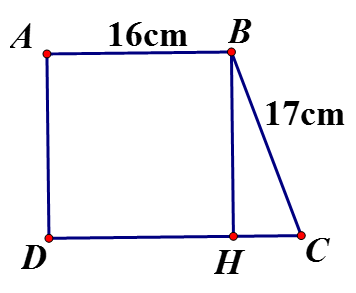
Hạ
Tứ giác ABHC có là hình chữ nhật
vuông tại H (định lý Pytago)
Mà AD=BH (vì là ABHC hình chữ nhật)
Suy raCâu 14:
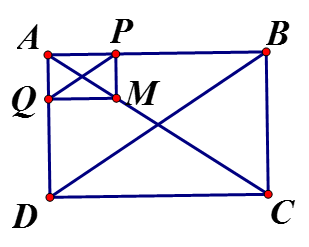
Vì ABCD là hình chữ nhật nên
Tứ giác APMQ có: là hình chữ nhật nên
Từ (1) và (2) mà hai góc ở vị trí đồng vị nên
Câu 15:
Sau khi thực hiện phép chia ta được dư là
Để thì dư bằng
