5 câu hỏi trắc nghiệm thuộc Dạng 2. Tìm độ dài đoạn thẳng, số đo góc

Bài tập Toán 8 Chủ đề 1 và 2: Tổng hợp định lí ta-lét, tam giác đồng dạng và các bài toán liên quan có đáp án

Dạng 2. Tìm độ dài đoạn thẳng, số đo góc

343 lượt thi
5 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Tính cạnh hình thoi biết AB= c, BC=a.

Xem đáp án

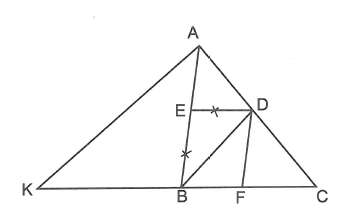
Gọi độ dài cạnh hình thoi là x.

Vì $E D / / B C$ nên $\frac{E D}{B C} = \frac{A E}{A B}$ (hệ quả định lý Ta-lét)

$\Rightarrow \frac{x}{a} = \frac{c - x}{c} \Leftrightarrow c x = a (c - x) \Leftrightarrow c x = a c - a x$

$\Leftrightarrow (a + c) x = a c \Leftrightarrow x = \frac{a c}{a + c}$

Vậy $x = \frac{a c}{a + c}$ .

Câu 2:

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Chứng minh

B D < \frac{2 a c}{a + c}

với AB= c, BC=a.

Xem đáp án

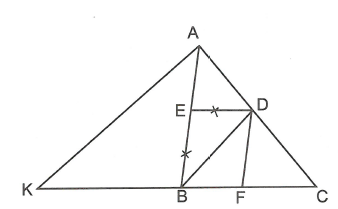
Trên tia đối của tia BC lấy điểm K sao cho $B K = B A$ .

Ta có tam giác ABK cân tại B nên $\hat{B K A} = \hat{B A K} = \frac{1}{2} \hat{A B C}$ (tính chất góc ngoài tam giác).

Mà $\hat{E B D} = \hat{D B F} = \frac{1}{2} \hat{A B C} \Rightarrow \hat{A K B} = \hat{D B F} \Rightarrow B D / / A K \Rightarrow \frac{B D}{A K} = \frac{C B}{C K}$ (hệ quả định lý Ta-lét)

$\Rightarrow \frac{B D}{A K} = \frac{C B}{B C + B K} = \frac{a}{a + c}$ (1)

Trong tam giác ABK có:

$A K < A B + B K = c + c = 2 c$ (định lý về độ dài cạnh trong tam giác) (2).

Từ (1) và (2) có: $B D < \frac{a}{a + c} .2 c = \frac{2 a c}{a + c}$

Vậy $B D < \frac{2 a c}{a + c}$ .

Câu 3:

Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).

Tính độ dài AB, BC, biết AD=m, DC=n, DE=d.

Xem đáp án

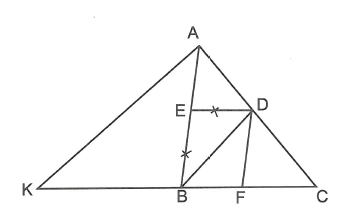
Vì $E D / / B C$ nên $\frac{E D}{B C} = \frac{A D}{A C}$ (hệ quả định lý Ta-lét)

Tương tự có $A B = \frac{d (m + n)}{n}$

Vậy $B C = \frac{d (m + n)}{m}$ và $A B = \frac{d (m + n)}{n}$ .

Câu 4:

Cho tam giác ABC, $P Q / / B C$ với P, Q là các điểm tương ứng thuộc AB, AC. Đường thẳng PC và QB cắt nhau tại G. Đường thẳng đi qua G và song song với BC cắt AB tại E và AC tại F. Biết $P Q = a, F E = b$ . Tính độ dài của BC.

Xem đáp án

Định hướng

Sau khi vẽ hình ta thấy hình thang PQCB có đủ các điều kiện của Ví dụ 2 - dạng 1 - chủ đề 1. Do đó ta có thể sử dụng kết quả của Ví dụ 2 để giải quyết bài toán.

Lời giải

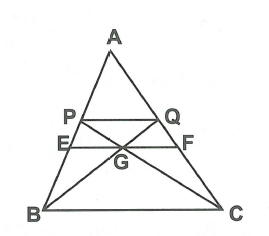
Đặt $B C = x$ .

Áp dụng kết quả của Ví dụ 2 - dạng 1 - chủ đề 1 ta có:

$\frac{1}{G E} = \frac{1}{G F} = \frac{1}{a} + \frac{1}{x} \Rightarrow G E = G F = \frac{a x}{a + x}$

$\Rightarrow G E + G F = 2 \frac{a x}{a + x} \Leftrightarrow E F = \frac{2 a x}{a + x} \Leftrightarrow b = \frac{2 a x}{a + x}$

$\Leftrightarrow a b + b x - 2 a x = 0 \Leftrightarrow x = \frac{a b}{2 a - b}$

Vậy $B C = \frac{a b}{2 a - b}$ .

Câu 5:

Trên cạnh BC của hình vuông ABCD cạnh 6, lấy điểm E sao cho $C F = 3$ . Trên tia đối của tia CD lấy điểm F sao cho . Gọi M là giao điểm của AE và BF. Tính góc AMC.

Xem đáp án

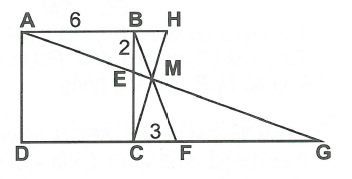
Gọi H là giao điểm của CM và AB, G là giao điểm của AM và DF.

Vì $A B / / C G$ nên $\frac{A B}{C G} = \frac{B E}{E C} = \frac{B E}{B C - B E} = \frac{2}{6 - 2} = \frac{1}{2}$ (hệ quả định lý Ta-lét)

$\Rightarrow C G = 2 A B = 2.6 = 12 \Rightarrow F G = C G - C F = 12 - 3 = 9$

Vì $A H / / C G$ nên $\frac{B H}{A B} = \frac{C F}{F G}$

$\Rightarrow \frac{B H}{6} = \frac{3}{9} \Rightarrow B H = 6. \frac{3}{9} = 2 \Rightarrow B H = B E$

Xét $Δ B A E$ và $Δ B C H$ có:

$\{\begin{cases} B E = B H (theo treân) \\ \hat{A B E} = \hat{C B H} = 90 ° \\ A B = B C (tính chát hình vuong) \end{cases}$

$\Rightarrow Δ B A E = Δ B C H (c . g . c) \Rightarrow \hat{B E A} = \hat{B H C} \Rightarrow \hat{A M C} = \hat{M A H} + \hat{A H M} = \hat{M A H} + \hat{A E B} = 90 °$

Vậy $\hat{A M C} = 90 °$ .

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 8 Chủ đề 1 và 2: Tổng hợp định lí ta-lét, tam giác đồng dạng và các bài toán liên quan có đáp án

Dạng 2. Tìm độ dài đoạn thẳng, số đo góc

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương