Dạng 3: Bài luyện tập 2 có đáp án dạng 1: Các Trường Hợp Đòng Dạng Của Tam Giác Vuông Suy Ra Từ Các Trường Hợp Đòng Dạng Của Tam Giác
-
604 lượt thi
-
11 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Hãy chỉ ra các cặp tam giác đồng dạng. Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng.
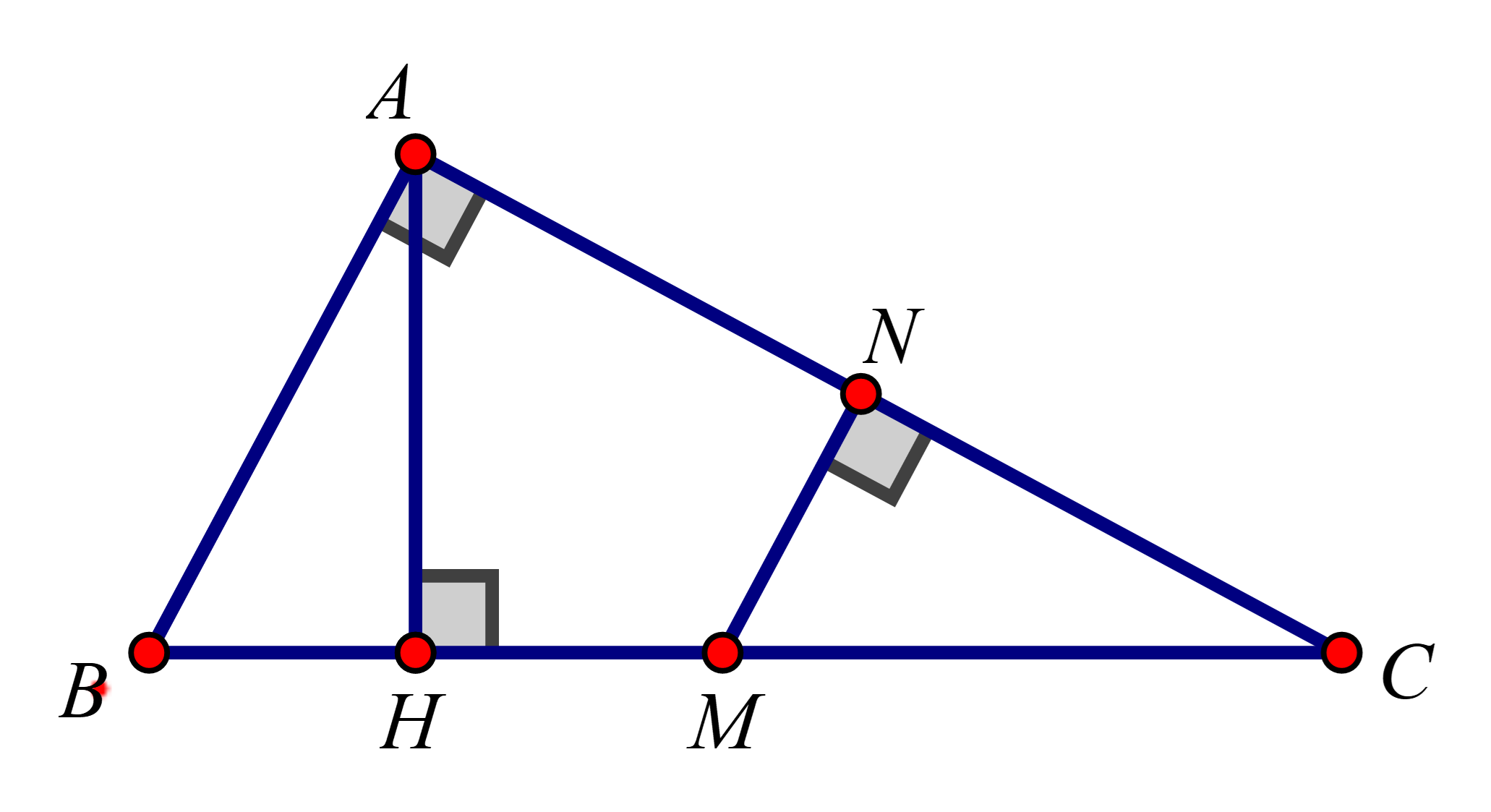
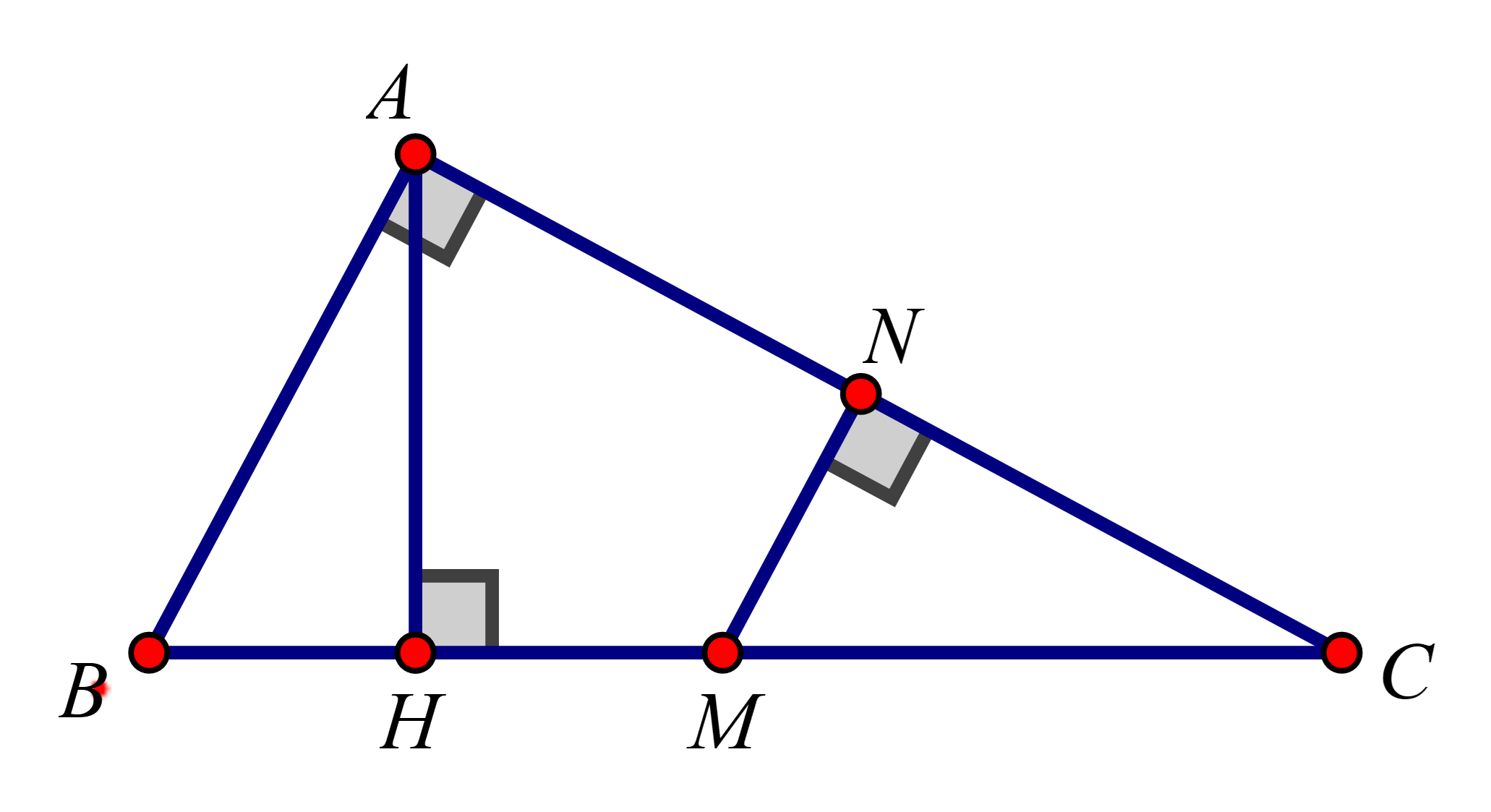
Trên hình có 4 tam giác vuông đồng dạng với nhau từng đôi một, vì chúng có các cặp góc nhọn tương ứng bằng nhau.
Đó là: ΔABC,ΔNMC,ΔHBA,ΔHAC (Bốn tam giác trên đã được viết theo các đỉnh tương ứng)
Câu 2:
Cho tam giác ABC vuông tại A có đường cao AH.Chứng minh rằng: AH2=BH.CH.
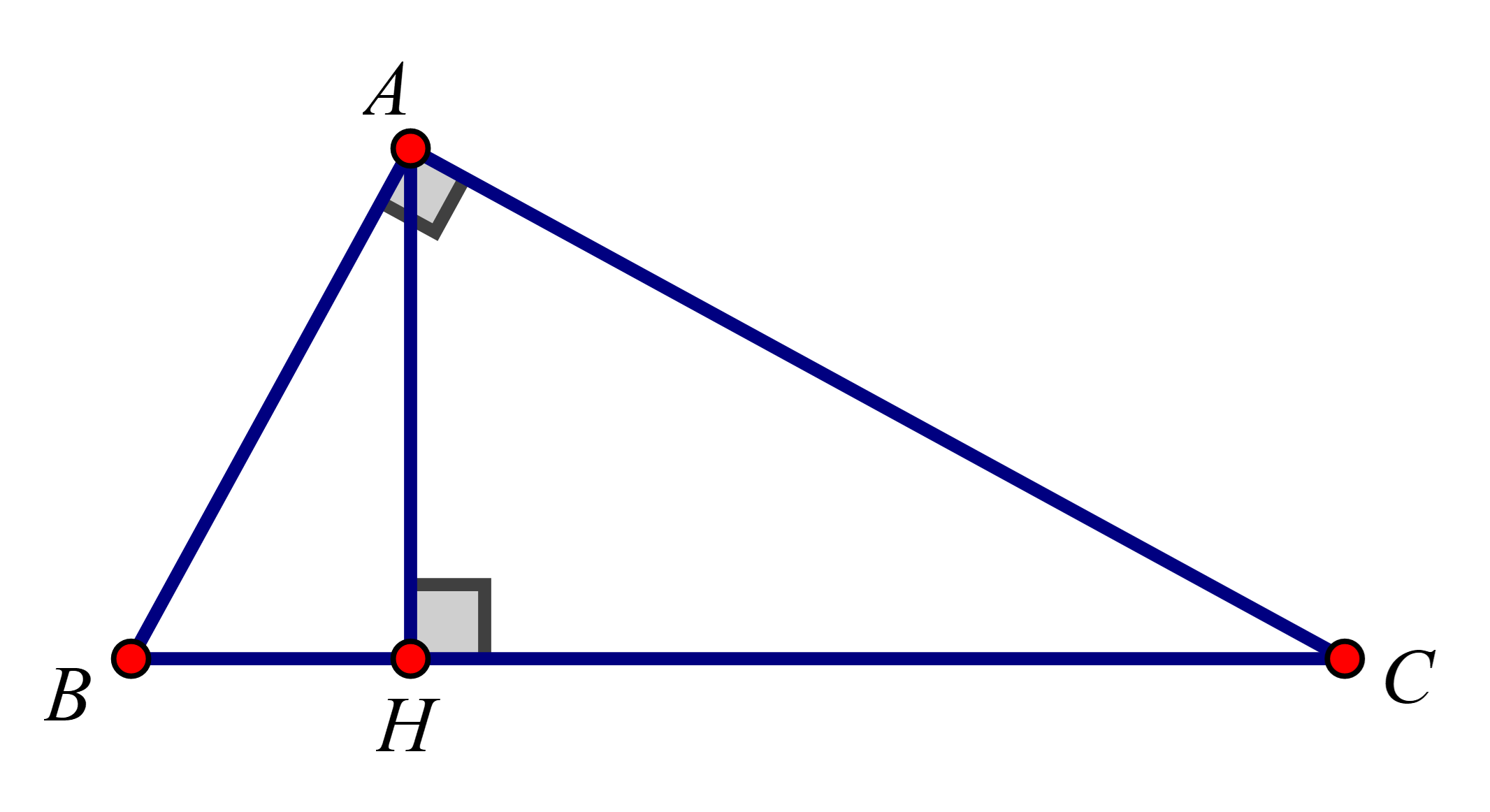
Xét tam giác vuông HBA và HAC có:
^BAH+^HAC=900^HCA+^HAC=900}⇒^BAH=^HCA
Suy ra ΔHBA∽ΔHAC
Từ đó: BHAH=AHCH⇒AH2=BH.CH
Câu 3:
Cho tam giác ABC vuông tại A, đường phân giác của góc B cắt AC tại D. Đường cao AH cắt BD tại I. Chứng minh rằng:AB.BI=BH.DB

1. BD là đừng phân giác nên ^ABD=^HBI mà ^DAB=^IHB=900
Suy ra ΔABD∽ΔHBI(g−g) ⇒ABHB=DBIB⇒AB.BI=BH.DB
Câu 4:
Cho tam giác ABC vuông tại A, đường phân giác của góc B cắt AC tại D. Đường cao AH cắt BD tại I. Chứng minh rằng: Tam giác AID cân.
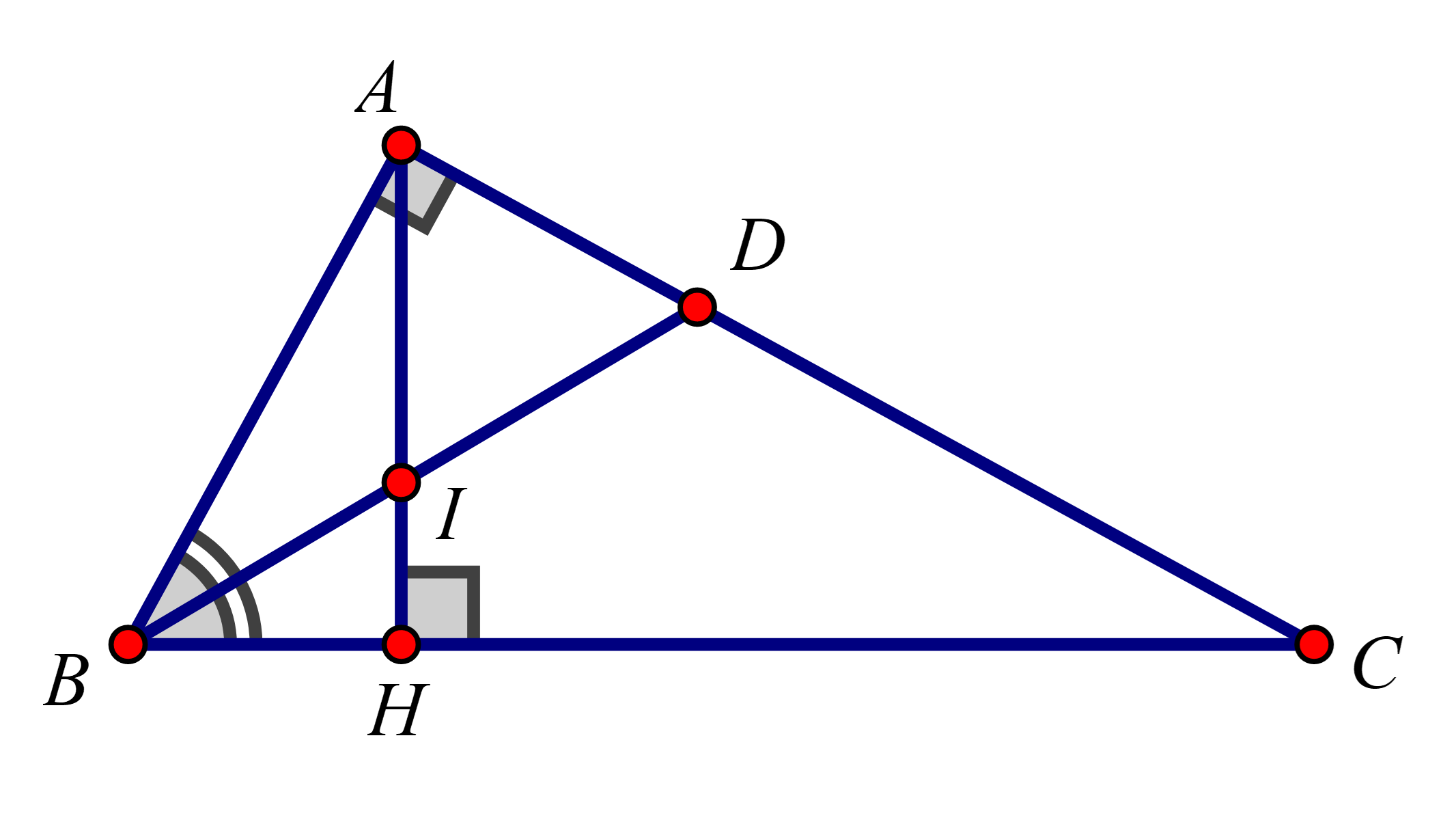
1. Do ΔABD∽ΔHBI(g−g) nên ^BDA=^BIH mà ^BIH=^DIA (đối đỉnh)
Suy ra : ^BDA=^DIA Do đó: Tam giác AID cân tại A.
Câu 5:
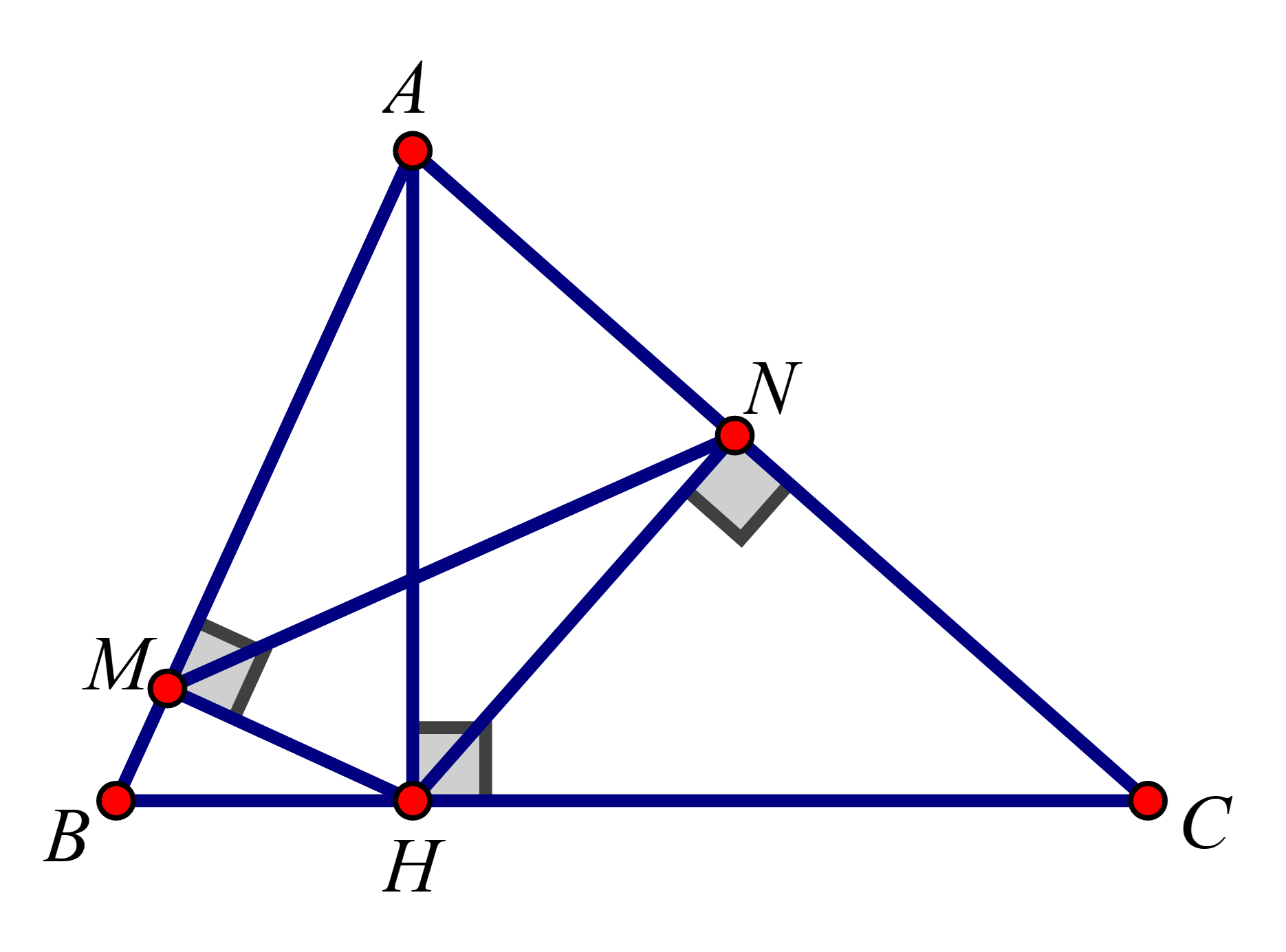
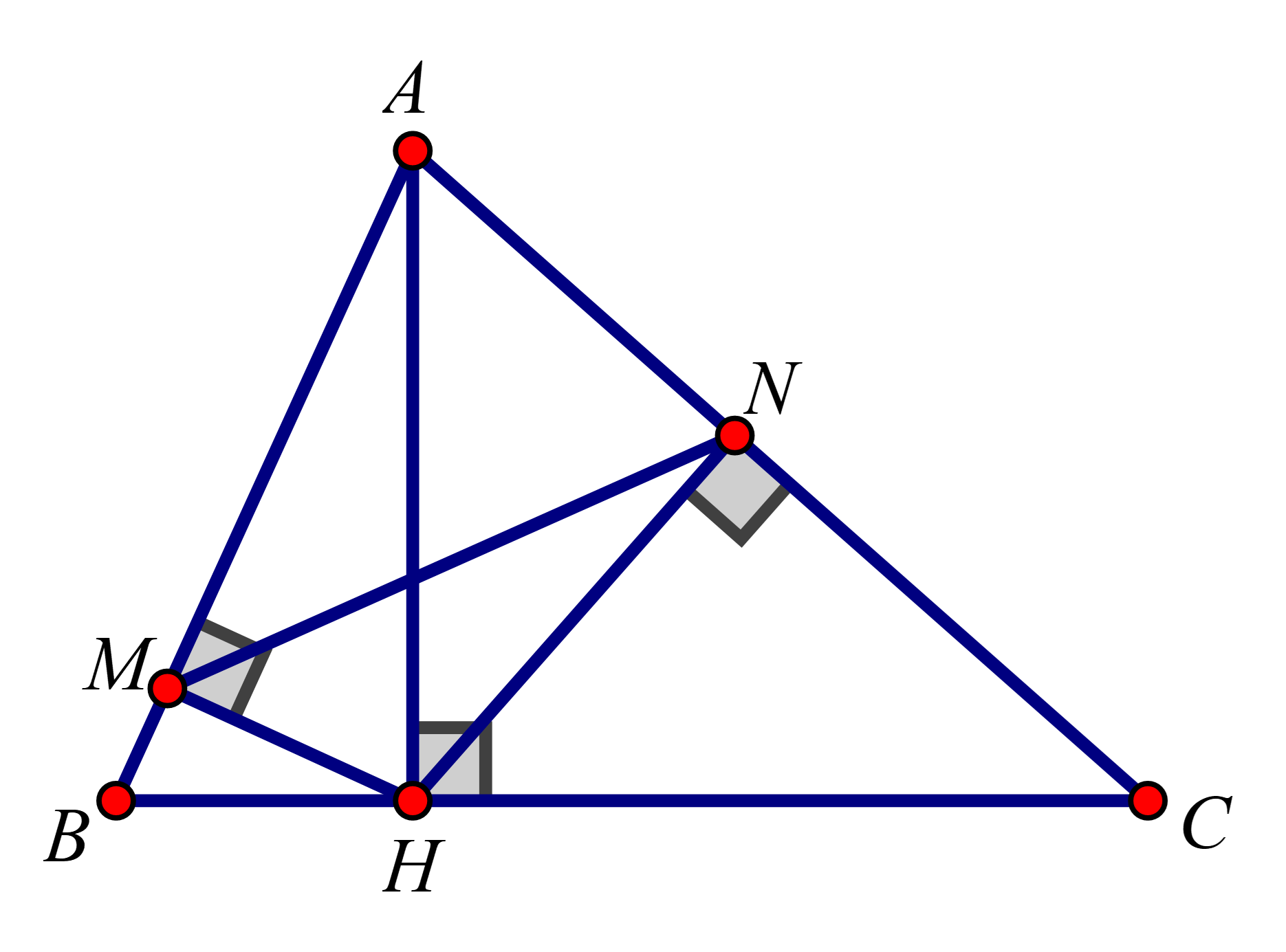
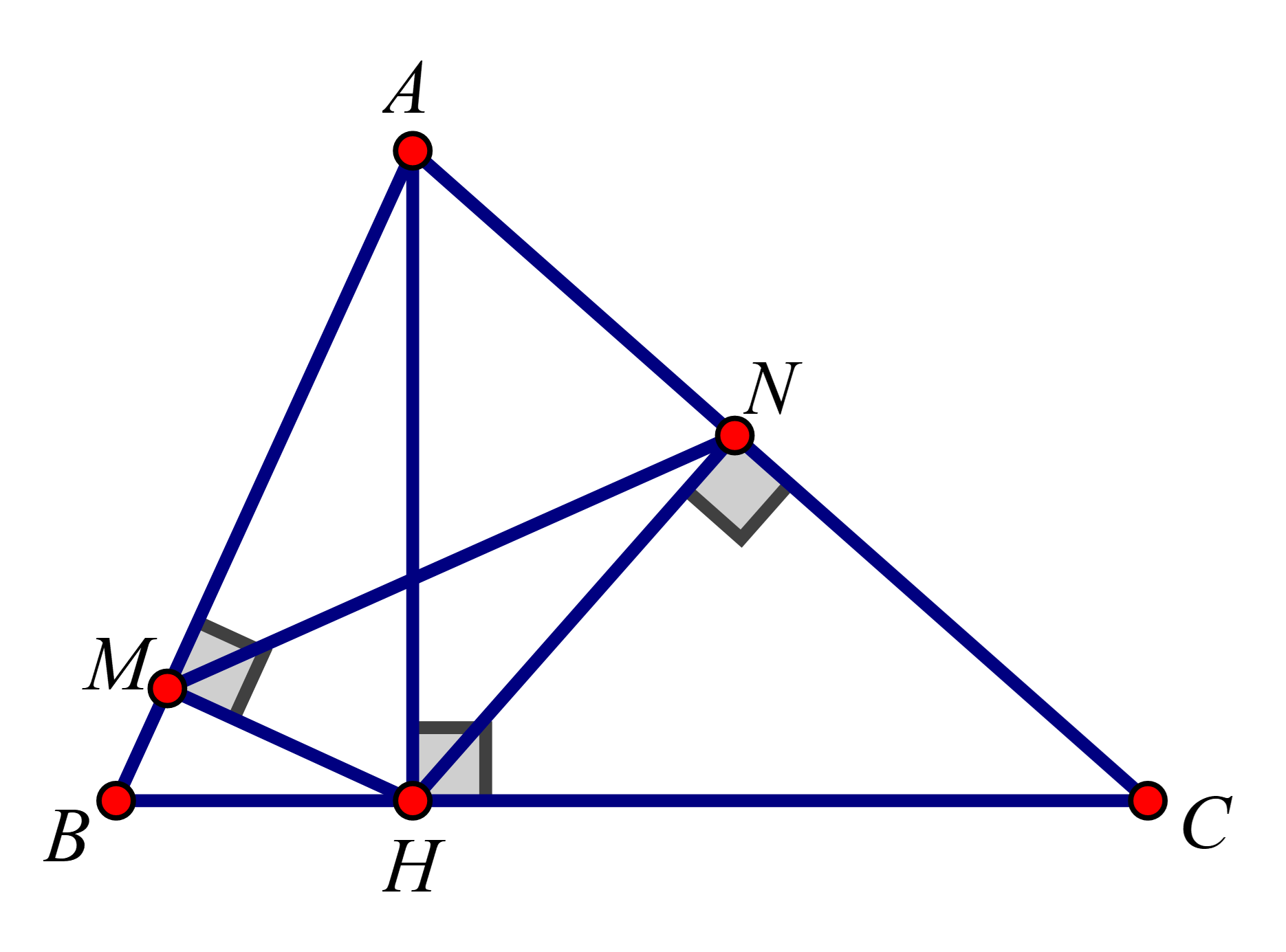
Cho tam giác ABC có 3 góc nhọn, biết AB=15cm,AC=13cm và đường cao AH=12cm. Gọi M,N lần lượt là hình chiếu vuông góc của H xuống AB và AC. CMR ΔAHN∽ΔACH
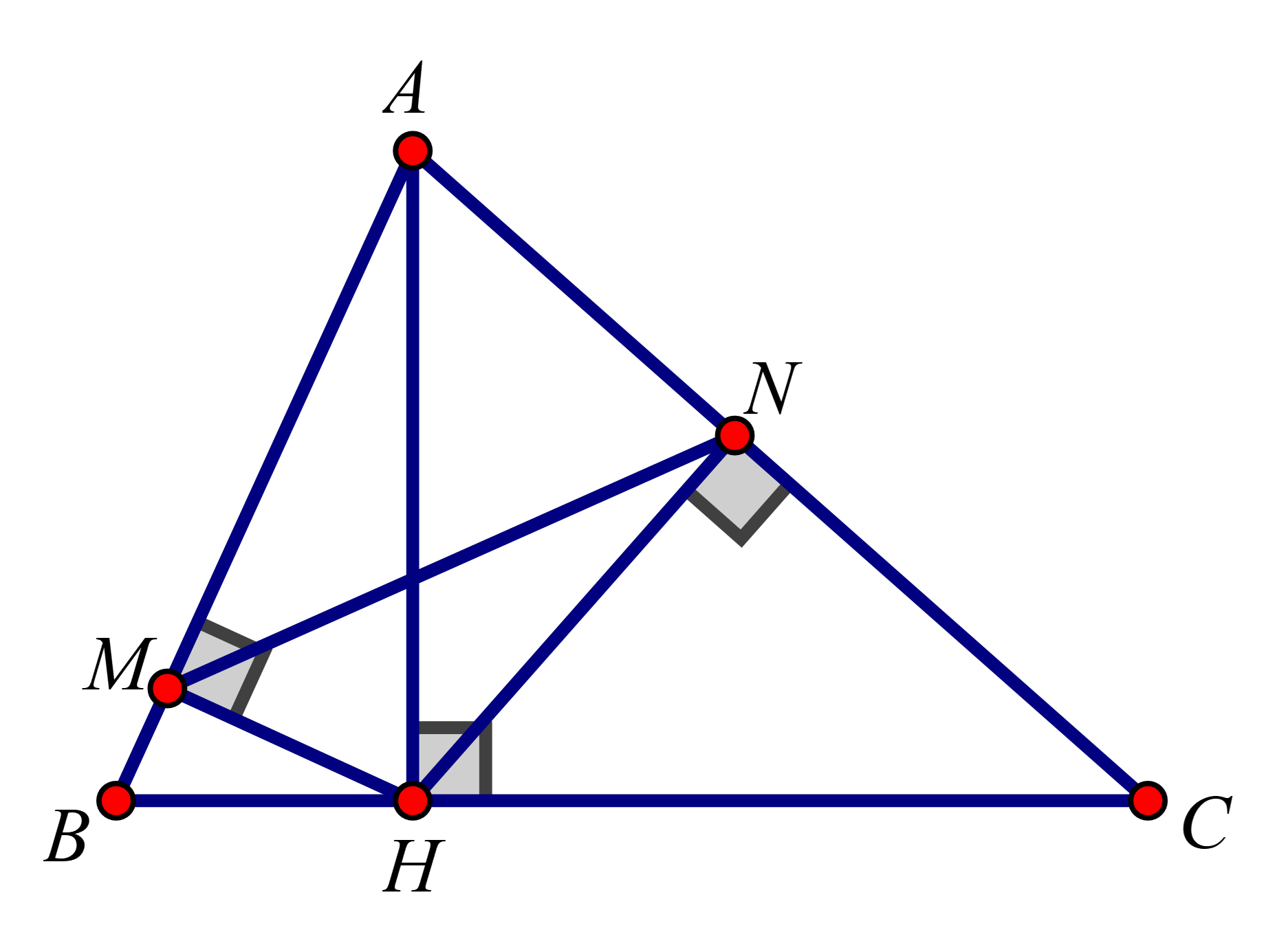
1. Ta có: ˆA−chung^ANH=^AHC=900}⇒ΔAHN∽ΔACH(g−g)
Câu 6:
Cho tam giác ABC có 3 góc nhọn, biết AB=15cm,AC=13cmvà đường cao AH=12cm. Gọi M,N lần lượt là hình chiếu vuông góc của H xuống AB và AC.Tính độ dài BC
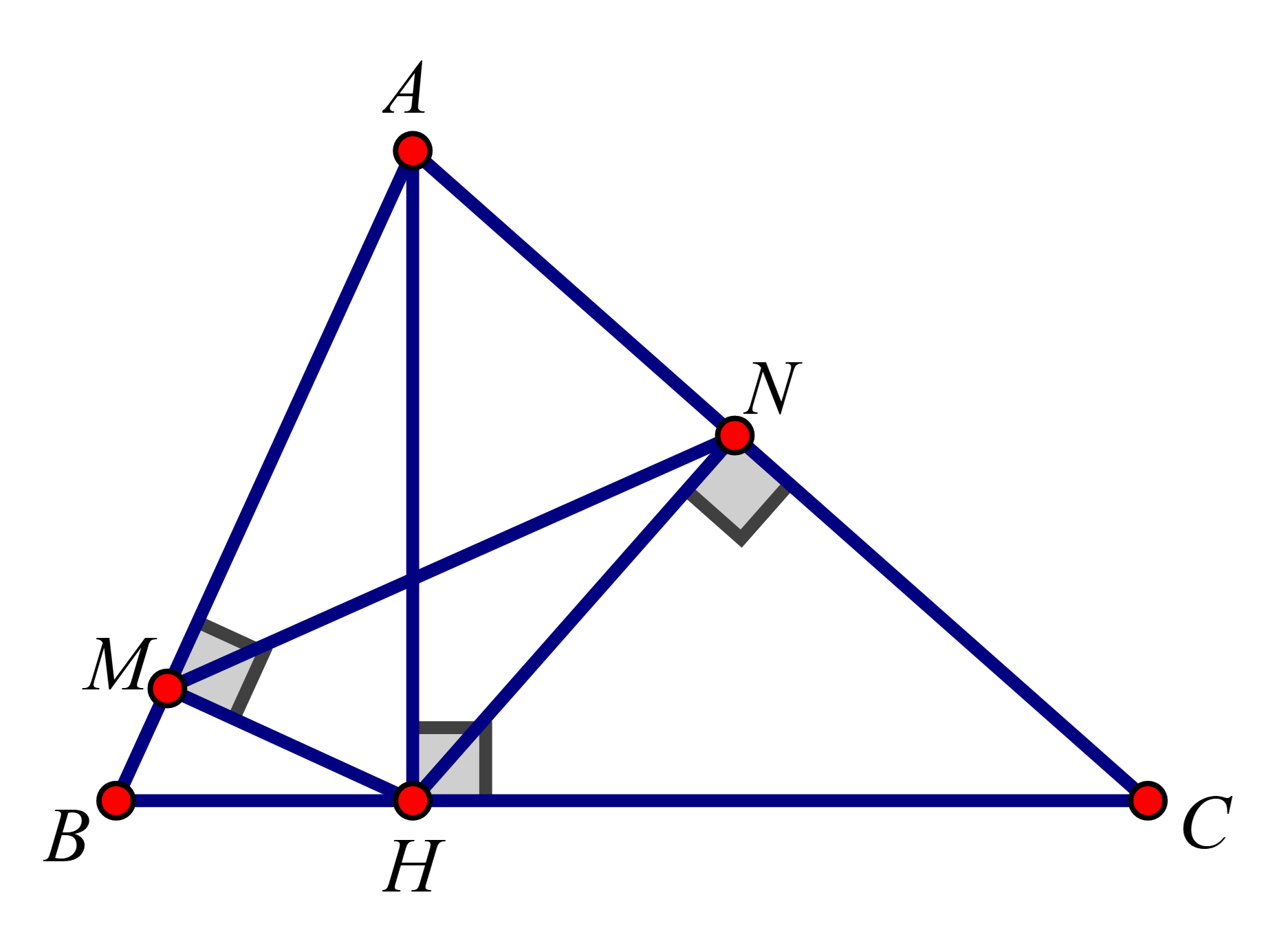
1. Xét tam giác vuông ABH có: BH=√AB2−AH2=√152−122=9(cm)
Xét tam giác vuông ACH có: CH=√AC2−AH2=√132−122=5(cm)
Khi đó: BC=BH+CH=9+5=14(cm)
Câu 7:
Cho tam giác ABC có 3 góc nhọn, biết AB=15cm,AC=13cm và đường cao AH=12cm. Gọi M,N lần lượt là hình chiếu vuông góc của H xuống AB và AC. Chứng minh: AM.AB=AN.AC, từ đó suy ra ΔAMN∽ΔACB .
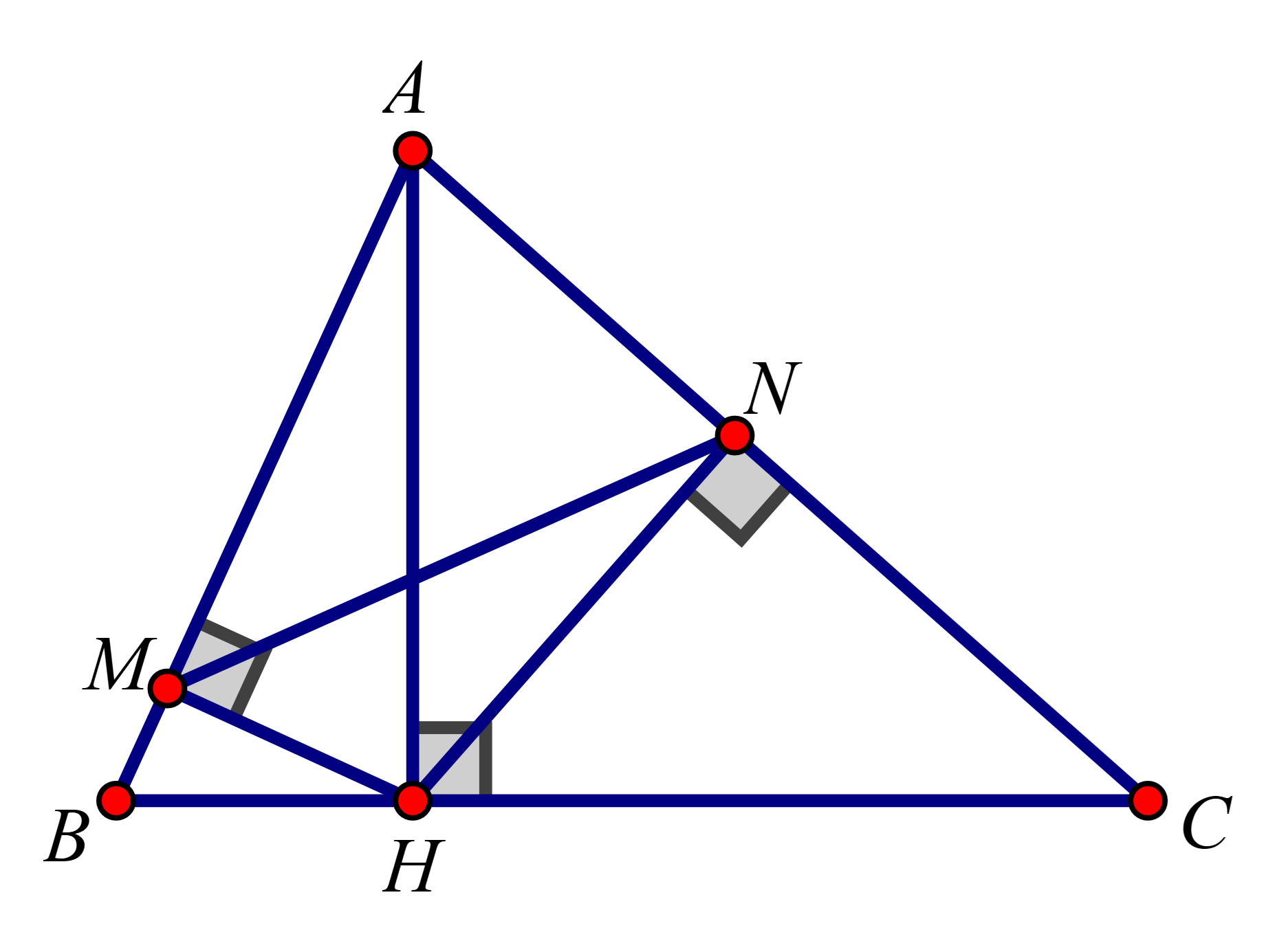
1. Do ΔAHN∽ΔACH⇒AHAC=ANAH⇒AH2=AC.AN(1)
Xét tam giác AMH và ABH có:
ˆA−chung^AMH=^AHB=900}⇒ΔAMH∽ΔAHB(g−g)
⇒AMAH=AHAB⇒AH2=AM.AB(2)
Từ (1),(2) ta có : AM.AB=AN.AC
Suy ra: AMAC=ANAB và ^MAN−chung
Nên ΔAMN∽ΔACB(c−g−c)
Câu 8:
Cho hình bình hành ABCD có AB=8cm,AD=6cm. Trên cạnh BC lấy điểm M sao cho BM=4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường DC tại N .Tính tỉ số IBID
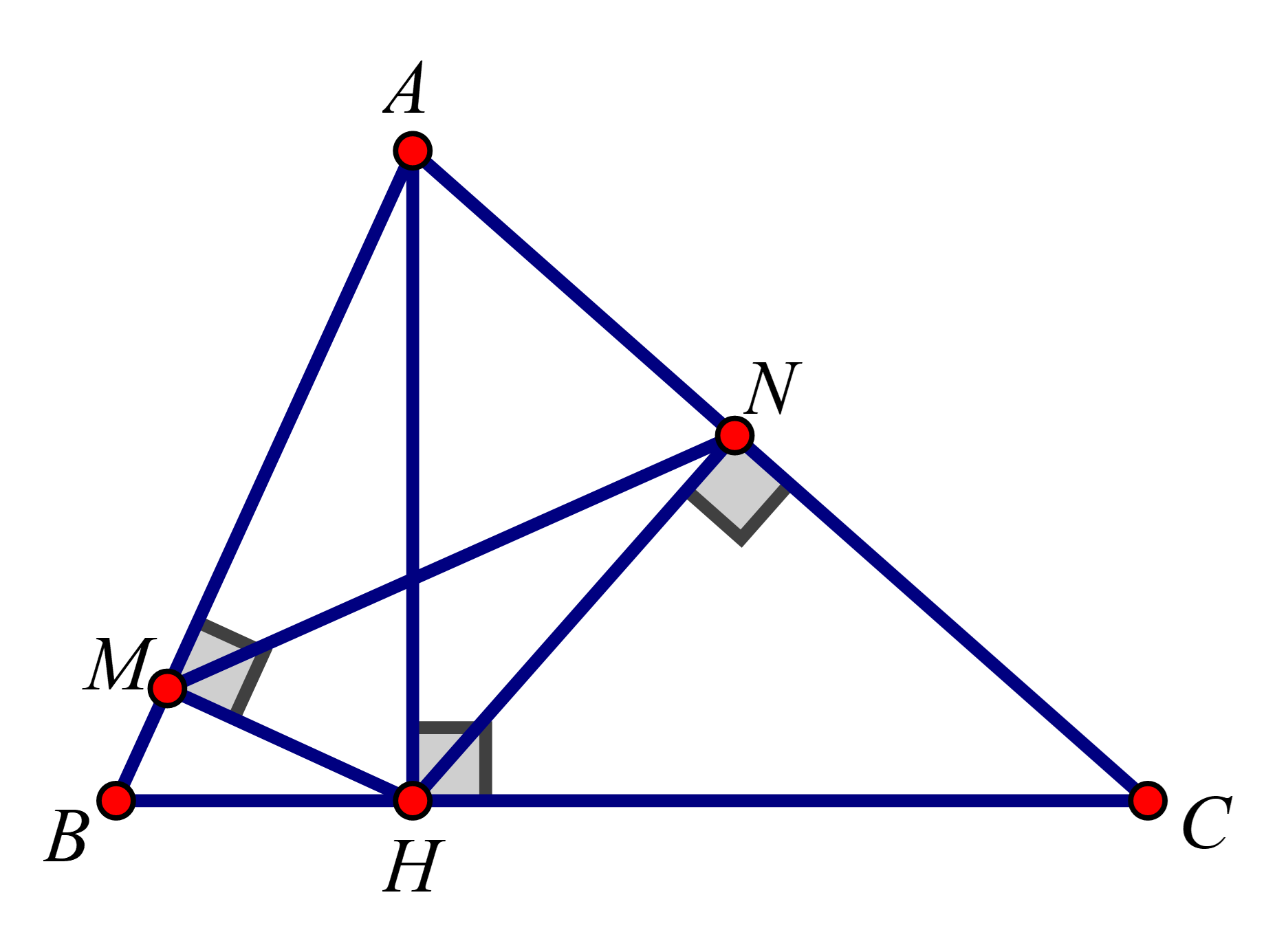
1. Ta có: BM//AD⇒BMAD=IBID=IMIA (Theo định lý Ta Let mở rộng)
Mà BMAD=46=23⇒IBID=23
Câu 9:
Cho hình bình hành ABCD có AB=8cm,AD=6cm. Trên cạnh BC lấy điểm M sao cho BM=4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường DC tại N. Chứng minh: ΔMAB∽ΔAND
1. Ta có: ^MAB=^AND(slt)^ABM=^NDA(hbh)}⇒ΔMAB∽ΔAND(g−g)
Câu 10:
Cho hình bình hành ABCD có AB=8cm,AD=6cm. Trên cạnh BC lấy điểm M sao cho BM=4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường DC tại N .Tính độ dài DN và CN
1. Do ΔMAB∽ΔAND nên MBAD=ABND⇒46=8ND⇒ND=6.84=12(cm)
Mà AB=DC=8(cm)(hbh)
Nên CN=DN−DC=12−8=4(cm)
Câu 11:
Đặt MP=NQ=x. Từ ΔBMQ∽ΔNCP ta tính được x = 6 cm.
Cạnh của hình vuông bằng 6 cm.
