Dạng 2: Bài luyện tập 1 có đáp án
-
624 lượt thi
-
18 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
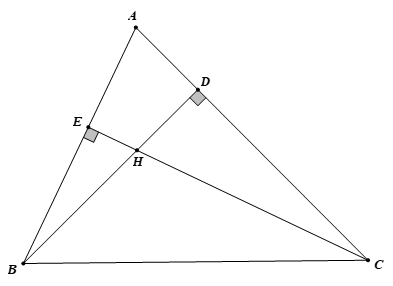
Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh:
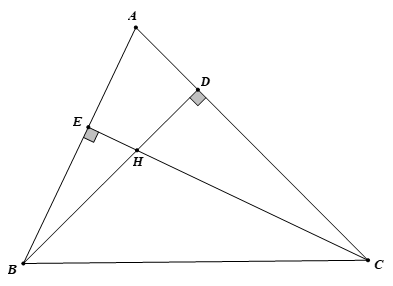
Có ta suy ra
Từ đó chứng minh được
Câu 3:
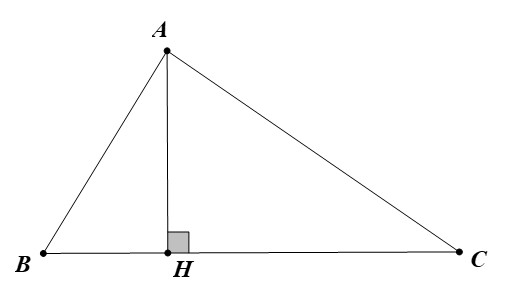
Cho có đường cao AH, biết ; Tính độ dài AH và chứng minh:
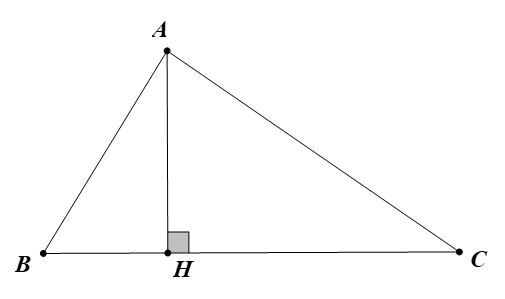
a) Vì vuông tại H, theo định lý Pitago ta có:
Vì vuông tại H, theo định lý Pitago ta có:
Ta lại có:
Xét và có:
Câu 7:
Cho hình vuông ABCD , cạnh a. Gọi E là điểm đối xứng với C qua D, EB cắt AD tại I. Trên EB lấy điểm M sao cho Chứng minh
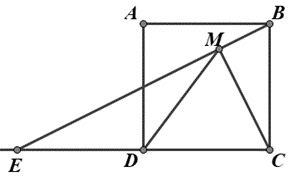
Chứng minh
Tam giác EMC có trung tuyến nên là tam giác vuông tại M.
Câu 8:
Cho hình vuông ABCD , cạnh a. Gọi E là điểm đối xứng với C qua D, EB cắt AD tại I. Trên EB lấy điểm M sao cho Chứng minh .
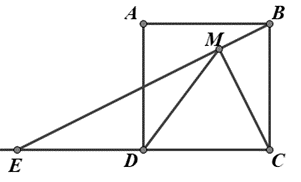
Chứng minh .
Câu 9:
Cho hình vuông ABCD , cạnh a. Gọi E là điểm đối xứng với C qua D, EB cắt AD tại I. Trên EB lấy điểm M sao cho Tính diện tích tam giác EMC theo a.
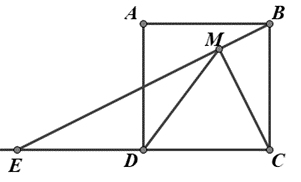
Tính diện tích tam giác EMC theo a.
Câu 11:
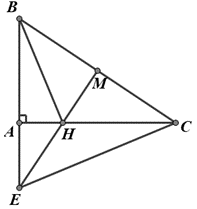
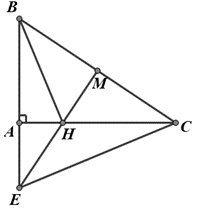
Cho tam giác ABC vuông ở A, AB = 5,4cm, AC = 7,2cm.Từ trung điểm M của BC, vẽ đường thẳng vuông góc với BC, cắt đường thẳng AC tại H và cắt đường thẳng AB tại E. Chứng minh DEMB ~ DCAB.
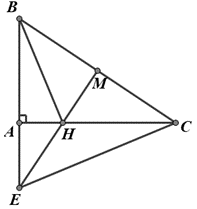
(góc chung) (g.g)
Câu 13:
Cho tam giác ABC vuông ở A, AB = 5,4cm, AC = 7,2cm. Chứng minh BH vuông góc với EC.
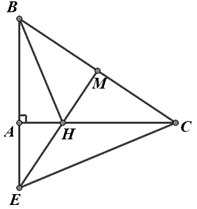
ΔBEC có 2 đường cao CA,EM cắt nhau tại H nên H là trực tâm ΔBEC,
Câu 14:
Cho tam giác ABC vuông ở A, AB = 5,4cm, AC = 7,2cm. Chứng minh
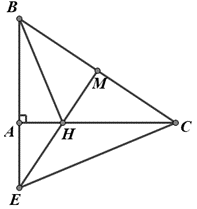
Chứng minh từ đó suy ra
Câu 15:
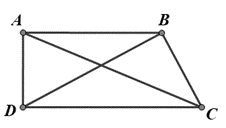
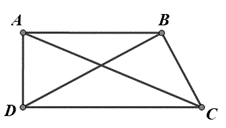
Cho tứ giác ABCD, có , , , , . Tính góc
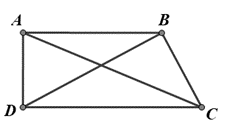
Ta có , suy ra tam giác ABD vuông tại A (Pitago đảo)
Câu 18:
Cho hình bình hành ABCD ( AC > BD) vẽ CE vuông góc với AB tại E, vẽ CF vuông góc với AD tại F.Chứng minh rằng

Vẽ Xét ABH và ACE có chung .
Suy ra
(1)
Xét và có (so le trong)
Suy ra (2)
Cộng vế theo vế (1) và (2) ta được: