Đề kiểm tra Giữa kì 1 Toán 8 có đáp án (Mới nhất)_ Đề số 2
-
730 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Kết quả phép tính x(x - y) + y(x + y) tại x = -3 và y = 4 là:
Thay x = -3 và y = -4 vào biểu thức x(x - y) + y(x + y) ta được:
(-3)(-3 - 4) + 4(-3 + 4) = 21 + 4 = 25
Chọn D.
Câu 2:
Khai triển biểu thức (x - 2y)3 ta được kết quả là:
Ta có:
(x - 2y3 = x3 - 3x2.2y + 3x.(2y)2 + (2y)3 = x3 - 6x2y + 12xy2 - 8y3
Chọn D.
Câu 3:
Giá trị biểu thức 20092 - 2018.2009 + 10092 có bao nhiêu chữ số 0 ?
20092 - 2018.2009 + 10092
20092 - 2.2009.1009 + 10092
= (2009 - 1009)2
= 10002
= 1000000
Vậy giá trị của biểu thức 20092 - 2018.2009 + 10092 có 6 chữ số 0.
Chọn A.
Câu 4:
4x2 - 12x + 9 = (2x)2 - 2.2x.3 + 32 = (2x - 3)2
Chọn A.
Câu 5:
Hình nào sau đây là tứ giác có hai đường chéo bằng nhau?
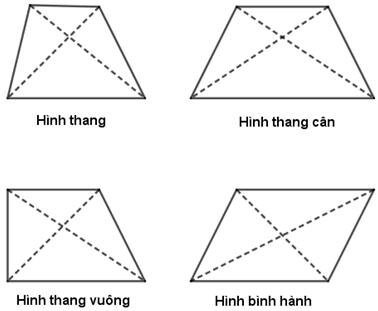
Quan sát hình vẽ, và áp dụng tính chất của các hình ta có: Hình thang cân là hình có hai đường chéo bằng nhau.
Chọn B.
Câu 7:
Cho hình bình hành ABCD có ∠A = 60o. Khi đó, hệ thức nào sau đây là không đúng?
Vì ABCD là hình bình hành nên ta có: ∠A = ∠C, ∠B = ∠D và AB // CD, AD // BC
Mà ∠A = 60o ⇒ ∠C = 60o
⇒ Đáp án C đúng.
Vì AD // BC mà ∠A và ∠B ở vị trí trong cùng phía nên ta có: ∠A + ∠B = 180o ⇒ ∠B = 120o
⇒ ∠B = 2∠C ⇒ Đáp án B đúng.
⇒ ∠A = ∠B/2 ⇒ Đáp án D đúng.
Vì AB // CD mà ∠A và ∠D ở vị trí trong cùng phía nên ta có: ∠A + ∠D = 180o ⇒ ∠D = 120o
⇒ Đáp án A sai.
Câu 8:
Hình chữ nhật có độ dài cạnh 5cm và 12cm thì khoảng cách từ giao điểm hai đường chéo đến mỗi đỉnh là

Chọn C.
Câu 9:
Rút gọn các biểu thức sau:
a. 2x(3x + 2) - 3x(2x + 3)
b. (x + 2)3 + (x - 3)2 - x2(x + 5)
c. (3x3 - 4x2 + 6x) : 3x
a. 2x(3x + 2) - 3x(2x + 3)
= 2x.3x + 2x.2 - 3x.2x - 3x.3
= 6x2 + 4x - 6x2 - 9x
= -5x
b. (x + 2)3 + (x - 3)3 - x2(x + 5)
= (x3 + 6x2 + 12x + 8) + (x2 - 6x + 9) - (x3 + 5x2)
= x3 + 6x2 + 12x + 8 + x2 - 6x + 9 - x3 - 5x2
= (x3 - x3) + (6x2 + x2 - 5x2) + (12x - 6x) + 9
= 2x2 + 6x + 9
c.
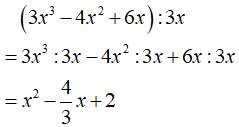
Câu 10:
Phân tích đa thức sau thành nhân tử: 2x3 - 12x2 + 18x
2x3 - 12x2 + 18x
= 2x(x2 - 6x + 9)
= 2x(x - 3)2
Câu 11:
Tìm x, biết: 3x(x - 5) - x2 + 25 = 0
3x(x - 5) - x2 + 25 = 0
3x(x - 5) - (x2 + 25) = 0
3x(x - 5) - (x + 5)(x - 5) = 0
(3x - x - 5)(x - 5) = 0
(2x - 5)(x - 5) = 0
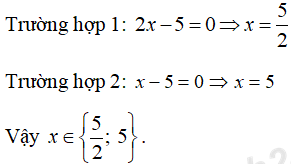
Câu 12:
Cho hình bình hành ABCD (AB > AD). Gọi E và K lần lượt là trung điểm của CD và AB. BD cắt AE, AC, CK lần lượt tại N, O và I. Chứng minh rằng:
a. Tứ giắc AECK là hình bình hành.
b. Ba điểm E, O, K thẳng hàng.
c. DN = NI = IB
d. AE = 3KI
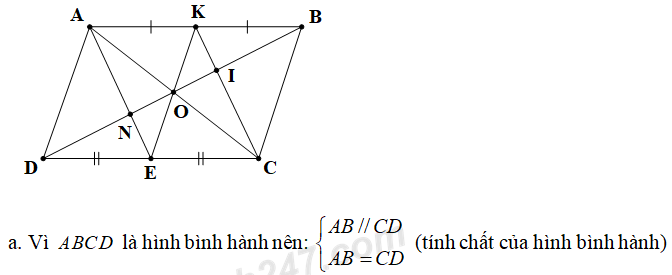
Mà E, K lần lượt là trung điểm của CD và AB nên AK = EC VÀ AK // EC.
⇒ Tứ giác AECK là hình bình hành (dấu hiệu nhận biết)
b. Trong hình bình hành ABCD có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD (tính chất của hình bình hành)
Mà AECK là hình bình hành nên O là trung điểm của EK.
⇒ Ba điểm E, O, K thẳng hàng.

Câu 13:
Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:
P = x2 + 5y2 + 4xy + 6x + 16y + 32
P = x2 + 5y2 + 4xy + 6x + 16y + 32
⇒ P = x2 + (4xy + 6x) + 5y2 + 16y + 32
⇒ P = x2 + 2x(2y + 3) + (2y + 3)2 - (2y + 3)2 + 5y2 + 16y + 32
⇒ P = [x + (2y + 3)]2 - 4y2 - 12y - 9 + 5y2 + 16y + 32
⇒ P = (x + 2y + 3)2 + y2 + 4y + 23
⇒ P = (x + 2y + 3)2 + (y + 2)2 + 19
Vì (x + 2y + 3)2 ≥ 0 với mọi x, y ∈ R
(y + 2)2 ≥ 0 với mọi y ∈ R
⇒ P = (x + 2y + 3)2 + (y + 2)2 + 19 ≥ 19 với mọi x, y ∈ R
Dấu "=" xảy ra khi và chỉ khi x + 2y + 3 = 0 và y + 2 =0
Suy ra, x = 1 và y = -2
Vậy P đạt giá trị nhỏ nhất bằng 19 tại x = 1 và y = -2.