Đề thi Học kì 2 Toán lớp 8 cực hay, có đáp án (Tự Luận - Trắc nghiệm - Đề 1)
-
2020 lượt thi
-
12 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm (2 điểm)
Trong các phương trình sau; phương trình nào là bậc nhất một ẩn?
Chọn D
Câu 8:
Cho ΔABC đồng dạng với ΔA'B'C'. Biết và hiệu số chu vi của ΔA’B’C’và chu vi của ΔABC là 30. Phát biểu nào đúng
Chọn A
Câu 9:
Phần tự luận (8 điểm)
Giải phương trình và bất phương trình sau :
a) Điều kiện: x ≠ 0 và x ≠ 1
MTC: x(x – 1)
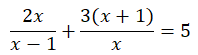
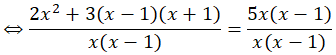
![]()
![]()
(thỏa mãn ĐKXD)
Tập nghiệm của (1): S = {3/5}
b) (2) ⇔ |1 – 2x| = 2x – 1 ⇔ |2x – 1| = 2x – 1
Ta biết |A| = A nếu A ≥ 0. Vậy 2x – 1 ≥ 0 ⇔ x ≥ 1/2
Tập nghiệm của (2) : S = {x | x ≥ 1/2}
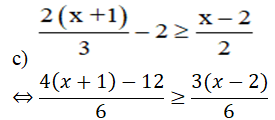
⇔4(x + 1) – 12 ≥ 3(x – 2)
⇔ 4x + 4 – 12 ≥ 3x – 6
⇔ 4x – 3x ≥ 8 – 6
⇔ x ≥ 2
Tập nghiệm: S = {x | x ≥ 2}
Câu 10:
Hai người cùng làm chung một công việc hết 12 ngày. Năng suất trong một ngày của người thứ hai bằng 2/3 năng suất người thứ nhất. Hỏi nếu làm một mình thì mỗi người phải làm trong bao lâu mới xong công việc ?
Gọi x là số ngày để người thứ nhất làm một mình xong công việc (x ∈ N*)
Một ngày người thứ nhất làm được 1/x công việc
Một ngày người thứ hai làm được
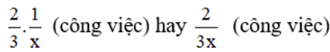
Một ngày cả hai người làm được
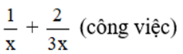
Hai người làm chung thì xong công việc trong 12 ngày nên một ngày cả 2 người làm được 1/12 công việc
Do đó, ta có phương trình:
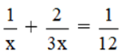
⇔ 12 + 8 = x ⇔ x = 20 (nhận)
Trả lời: Người thứ nhất làm trong 20 ngày; người thứ hai làm trong 30 ngày.
Câu 12:
Cho tam giác ABC có ba góc nhọn, biết và đường cao Gọi N, M lần lượt là hình chiếu vuông góc của H xuống AC và AB.
a) Chứng minh rằng ΔAHN ∼ ΔACH
b) Tính độ dài BC
c) Chứng minh ΔAMN ∼ ΔACB
d) Tính MN

a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
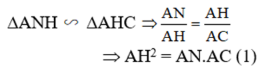
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
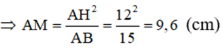
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()