Trắc nghiệm chuyên đề Toán 8 Chủ đề 6: Các trường hợp đồng dạng của tam giác vuông có đáp án
Trắc nghiệm chuyên đề Toán 8 Chủ đề 6: Các trường hợp đồng dạng của tam giác vuông có đáp án
-
260 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Hướng dẫn giải:
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có:
Vậy SABC = 1/2AB.AC = 1/2.2√(13) .3√(13) = 39( cm2 )
Chọn đáp án A.
Câu 2:
Hướng dẫn giải:
Ta có:
⇒ Δ ABC ∼ Δ MNP ( c - g - c )
Chọn đáp án D.
Câu 3:
Hướng dẫn giải:
Áp dụng tính chất mở rộng
Nếu hai tam giác đồng dạng với nhau thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng.
+ Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng.
+ Tỉ số các chu vi bằng tỉ số đồng dạng.
Đáp án D sai.
Chọn đáp án D.
Câu 4:
Hướng dẫn giải:
Ta có:
⇒ Δ ABC ∼ Δ DFE ( c - g - c )
Chọn đáp án C.
Câu 5:
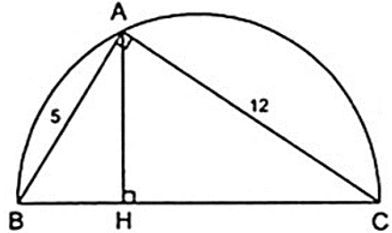
Cho hình bên là tam giác ABC vuông tại A, đường cao AH
a) Trong hình bên có bao nhiêu cặp tam giác đồng dạng với nhau. Hãy chỉ ra các cặp đồng dạng và theo các đỉnh tương ứng.
b) Cho biết AB = 5cm, AC = 12cm. Tinh độ dài các đoạn thẳng BC, AH, BH và CH.
Hướng dẫn giải:
a) Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.
b) Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta có:
BC2 = CA2 + AB2 ⇒ BC2 = 122 + 52 = 132 ⇔ BC = 13( cm )
Vì SABC = 1/2AB.AC = 1/2AH.BC ⇒ AH.BC = AB.AC
Hay 12.5 = AH.13 ⇒ AH = 60/13 ( cm )
Từ câu a ta có: Δ BHA ∼ Δ BAC ⇒ BH/BA = BA/BC hay BH/5 = 5/13 ⇔ BH = 25/13( cm )
Do đó: CH = BC - BH = 13 - 25/13 = 144/13( cm )
Câu 6:
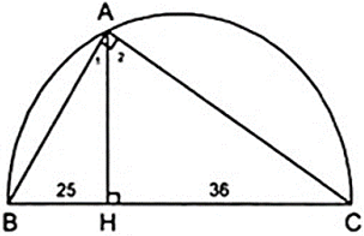
Chân đường cao AH chia cạnh huyền BC thành hai đoạn thẳng có độ dài lần lượt là 25 cm và 36 cm. Tính chu vi và diện tích của tam giác đó.
Hướng dẫn giải:
Ta có: Δ AHB ∼ Δ CHA ⇒ AH/HC = HB/HA
Hay HA/36 = 25/HA ⇔ HA2 = 302 ⇒ HA = 30( cm )
Ta có: SABC = 1/2AH.BC = 1/2.30.61 = 915( cm2 )
Áp dụng định lý Py – ta –go ta được:
