Bài tập Toán 8 Chủ đề 5: Đường trung bình của tam giác, của hình thang có đáp án
Dạng 3. Sử dụng phối hợp đường trung bình của tam giác và đường trung bình của hình thang đê chứng minh có đáp án
-
684 lượt thi
-
4 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình thang ABCD (AB//CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, BD, AC, BC. Chứng minh:
a) M, N, P, Q cùng nằm trên một đường thẳng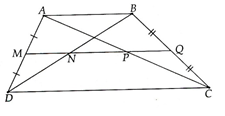
a) Ta có MN là đường trung bình của tam giác ABD
=> MN // AB
Tương tự, ta được MP//CD và MQ//AB, CD.
Như vậy, MN, MP, MQ cùng song song AB Þ ĐPCM.
Câu 3:
Cho hình thang ABCD (AB//CD) với AB = a, BC = b, CD = c và DA = d. Các tia phân giác của góc A và góc D cắt nhau tại E, các tia phân giác của và cắt nhau tại F. Gọi M, N theo thứ tự là trung điểm của AD và BC.
a) Chứng minh M, E, N, F cùng nằm trên một đường thẳng.
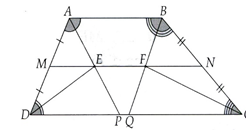
a) Gọi P và Q lần lượt là giao điểm của AE, AF với CD.
Chứng minh tương tự 4.
Câu 4:
b) Tính độ dài MN, MF, FN theo a, b, c, d.
b) Ta có:
Lại có:
c = CD = CQ + QD = BC + QD = b + QD (do tam giác BCQ cân) Þ QD = c - b.Trong hình thang ABQD có M là trung điểm của AD và MF//DQ nên chứng minh được F là trung điểm của BQ, từ đó chứng minh MF là đường trung bình của hình thang ABQD.
Vì MF là đường trung bình của hình thang ABQD.
Þ
Mặt khác, FN là đường trung bình của tam giác BCQ, tức là
