Bài tập Toán 8 Chủ đề 5: Đường trung bình của tam giác, của hình thang có đáp án
Dạng 6. Bài tập tự luyện đường trung bình của hình thang có đáp án
-
682 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho và đường thẳng d qua A không cắt đoạn thẳng BC. Vẽ . Gọi I là trung điểm của BC.Chứng minh ID = IE.
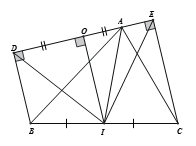
BD // AE (cùng vuông góc với d)
Tứ giác BDEC là hình thang,
Từ I kẻ
Hình thang BDECcó IO // BD // CE và IB = IC nên OD = OE
Ta có OD = OE; nên IO là đường trung trực của đoạn thẳng DE => ID = IE
Câu 2:
Cho hình thang vuông ABCD tại A và D Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) cân tại F
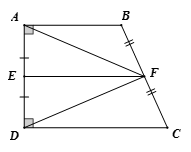
a) Chỉ ra EF là đường trung bình của hình thang ABCD nên EF // AB // CD
. AE = ED , EF là đường trung trực của AB nên FA = FD hay cân tại F
Câu 4:
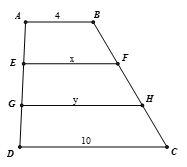
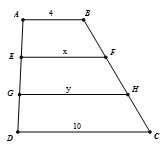
Theo tính chất của đường trung bình của hình thang,
ta có hay:
(1)
và (2)
Từ (1) và (2) suy ra
Ta tính được x = 6 và y = 8
Câu 5:
Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N.
a, Chứng minh rằng N, E, F lần lượt là trung điểm của BC, BD, AC.
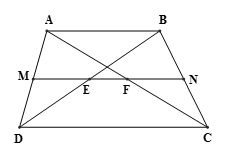
a) Xét hình thang ABCD có MA = MD ; => N là trung điểm của BC
Xét có MA = MD; MF // DC => FA = FC
Xét có MA = MD; MF // DC => ED = EB
Câu 6:
b, Gọi I là trung điểm của AB , đường thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh : KC = KD .
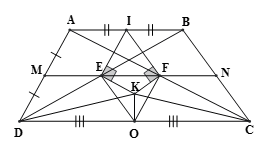
b) IE là đường trung bình của MA = MD; MF // DC => FA = FC
OF là đường trung bình của MA = MD; MF // DC => ED = EB
Vậy IE // FO
Có
Chứng minh tương tự ta có IF // EO // BC ;
có ; nên K là trực tâm mà ; vậy KO là đường trung trực của DC hay KC = KDCâu 7:
Cho hình thang ABCD, AB là đáy nhỏ. Gọi M, N, P, Q lần lượt là trung điểm của AD, BC, BD và AC.
a) Chứng minh bốn điểm M, N, P, Q thẳng hàng;
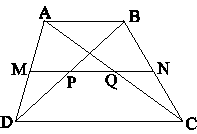
a) Xét ABD có MP là đường trung bình
Þ MP // AB Þ MP // CD.
Xét DADC có MQ là đường trung bình Þ MQ // CD.
Xét hình thang ABCD có MN là đường trung bình
=> MN // CD.
Qua điểm M có các đường thẳng MP, MQ, MN cùng song song với CD nên các đường thẳng này trùng nhau, suy ra bốn điểm M, N, P, Q thẳng hàng.
Câu 9:
c) Hình thang ABCD phải có điều kiện gì để MP = PQ = QN.
c) Ta có
(đáy lớn gấp đôi đáy nhỏ).
Câu 10:
Cho hình thang ABCD (AB//CD), tia phân giác của góc C đi qua trung điểm M của cạnh bên AD. Chứng minh rằng:
a)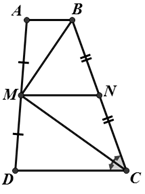
a) Gọi N là trung điểm BC.
Ta có
Mà (vì CM là phân giác ![]() )
)
Suy ra
Tam giác MCN cân tại N , do đó MNB cân tại N . Mặt khác , suy ra
Câu 11:
b) Vì MN là đường trung bình của hình thang ABCD nên
Ta lại có . Do đó BC = AB + CDCâu 12:
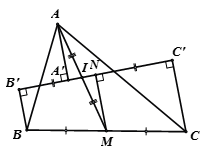
Gọi N là hình chiếu của M trên d.
Xét tứ giác BB'C'C có BB' // CC' (cùng vuông góc d)
=> BB'C'C là hình thang.
M là trung điểm BC và MN // BB' // CC' (cùng vuông góc d)
=> MN là đường trung bình của hình thang => BB'C'C
(1) ![]()
Chứng minh được (2)
Từ (1); (2)suy ra BB' + CC' = 2AA'