Dạng 3: Bài luyện tập 1 có đáp án
-
575 lượt thi
-
17 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
Cho , phân giác Ot. Trên Ox lấy các điểm A và C' sao cho , trên Oy lấy các điểm A' và C sao cho trên tia Ot lấy các điểm B và B' sao cho Chứng minh:
Chứng minh được
Câu 3:
Cho , phân giác Ot. Trên Ox lấy các điểm A và C' sao cho , trên Oy lấy các điểm A' và C sao cho trên tia Ot lấy các điểm B và B' sao cho Chứng minh:
Chứng minh được
Câu 4:
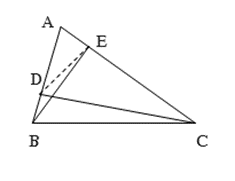
Xét tam giác AEB và tam giác ADC có
;
Mặt khác lai có góc A chung
(c-g-c)
Câu 5:
Cho ABC có , ,. Gọi D và E là hai điểm lần lượt trên các cạnh AB, AC sao cho , . Chứng minh :

Chứng minh tương tự câu a) ta có
(hai góc tương ứng)
Câu 6:
Cho ABC có , . Gọi D và E là hai điểm lần lượt trên các cạnh AB, AC sao cho , . Chứng minh :
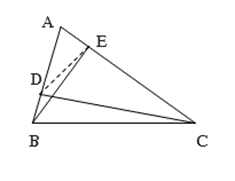
Theo câu b) ta có
Câu 7:
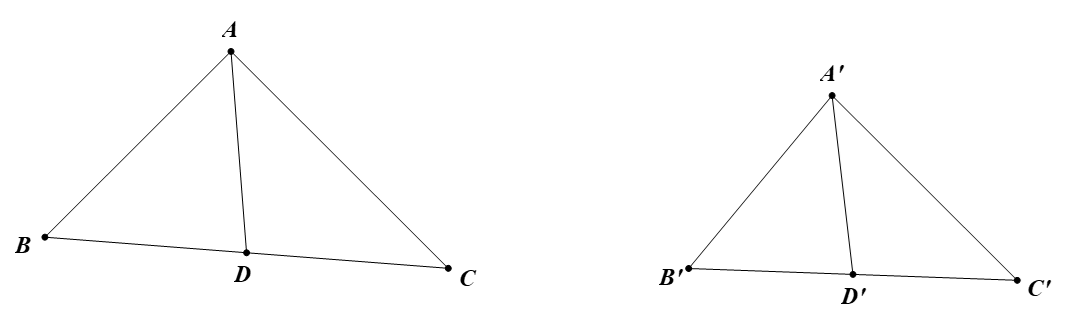
có AD và lần lượt là trung tuyến xuất phát từ đỉnh A và A’ xuống cạnh BC và B’C’ của hai tam giác đó.
Ta có . Có .
Vậy (c-g-c) Từ đó suy ra
Câu 8:
Cho tam giác ABC có Chứng minh
Trên tia đối của tia BA lấy điểm E sao cho . Chứng minh được
suy ra
Từ đó ta có
Câu 9:
Cho hình thoi ABCD có . Gọi M là một cạnh thuộc cạnh AD. Đường thẳng CM cắt đường thẳng AB tại N. Chứng minh
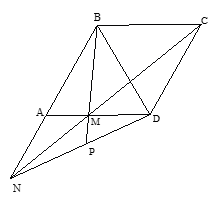
Ta có ( do AD // BC) suy ra hay (1) (vì BC = AB).Ta có NA // DC ( do AB // DC) suy ra hay (2) (vì ).
Từ (1) và (2) suy ra hay .
Câu 10:
Cho hình thoi ABCD có . Gọi M là một cạnh thuộc cạnh AD. Đường thẳng CM cắt đường thẳng AB tại N. BM cắt DN tại P. Tính góc .
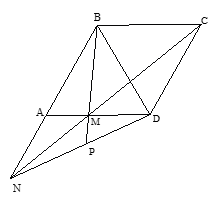
Từ
Xét BND và DBM có và .
Suy ra
Mà nên .
Câu 11:
Cho tam giác ABC có ; ; . Chứng minh rằng: .
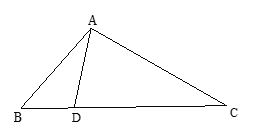
Trên đoạn thẳng BC lấy điểm D sao cho
Þ Þ nên cân tại C, do vậy (1)
và có chung và
Suy ra (c.g.c) Þ(2)
Từ (1) và (2) ta có :
Do đó .
Câu 12:
Cho cân tại A. Lấy M tùy ý thuộc BC, kẻ MN song song với AB (với N ∈ AC), kẻ MP song song với AC ( với P ∈ AB). Gọi O là giao điểm của BN và CP. Chứng minh rằng .

Giả sử . Gọi Q là giao điểm MO và AB ; K là giao điểm CP và MN.
Vì là hình bình hành nên (1)
Vì ∆ABC cân tại A nên suy ra cân tại P và cân tại N.
Do đó và kết hợp với , suy ra (2)
Từ (1) và (2) suy ra (c.g.c) Þ hay . Điều phải chứng minh