Dạng 4: Bài luyện tập 2 có đáp án
-
567 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
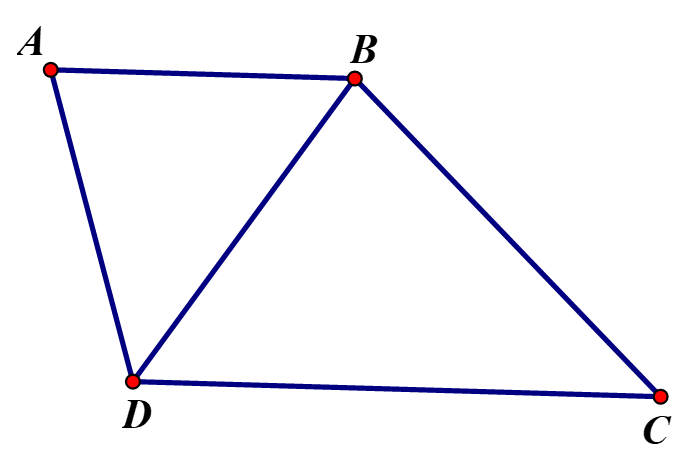
Cho có. Gọi D là trung điểm của thuộc cạnh AC sao cho Chứng minh rằng:
Xét và ta có:
chung
Hay (c - g - c)
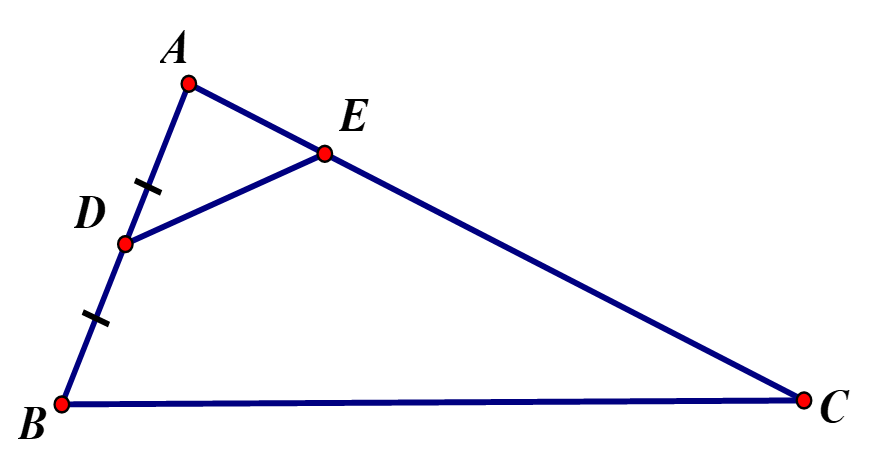
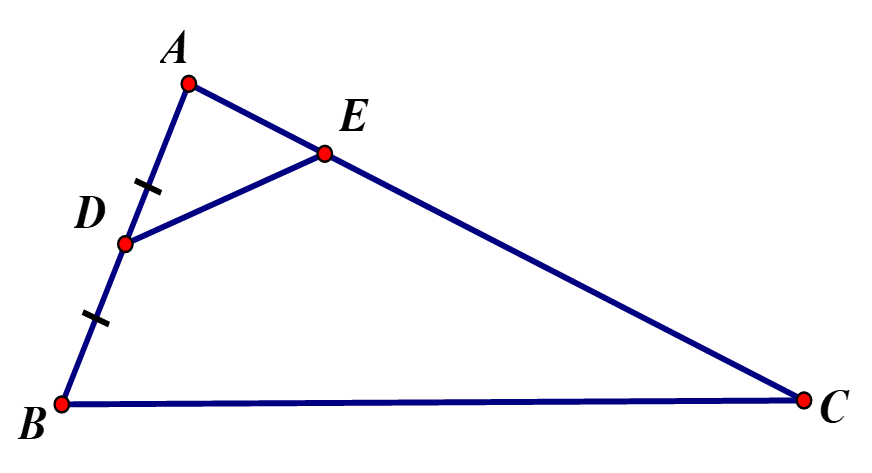
Câu 2:
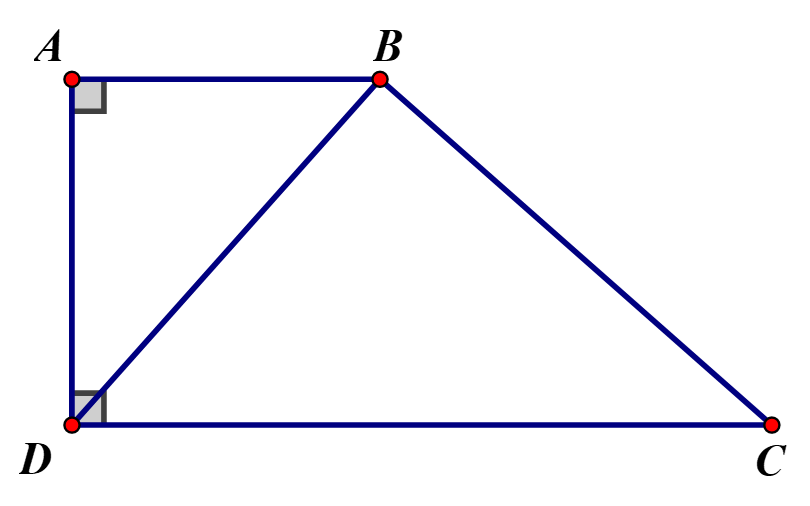
Cho có. Gọi D là trung điểm của thuộc cạnh AC sao cho Tính độ dài DE.
Vì nên ta có:
Câu 4:
Cho hình thoi ABCD có góc . Qua C kẻ đường thẳng d cắt tia đối của các tia BA,DA theo thứ tự ở E,F. Chứng minh rằng:
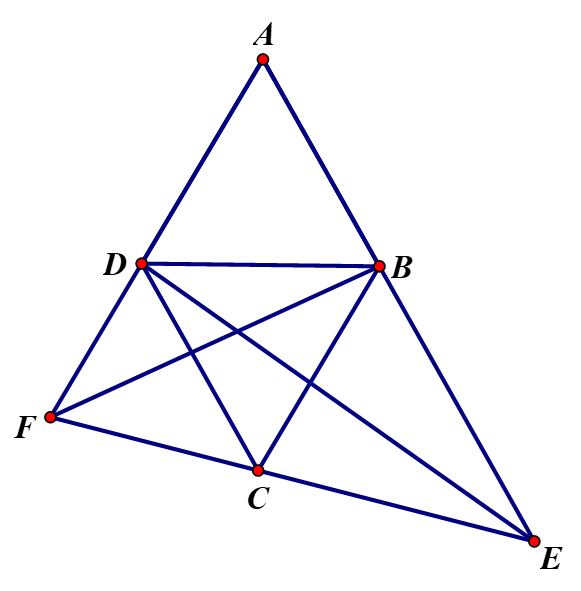
Do nên ta có:
Mà nên ta có:
Do đó:
Câu 5:
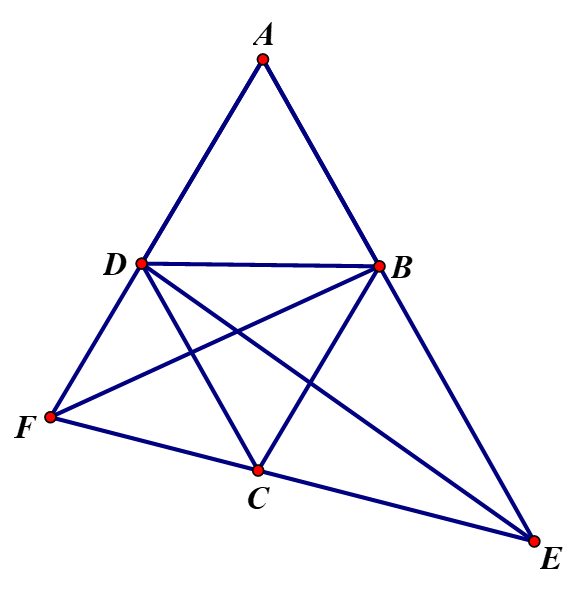
Vì theo a ta có:
Mà = 1200
Do đó (c - g - c)Câu 6:
Cho ABC có, Tính AC
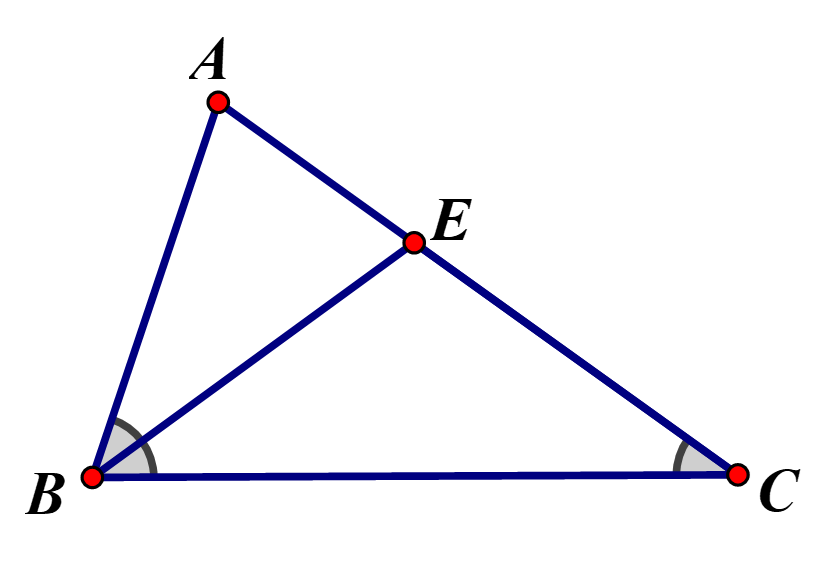
Vẽ tia phân giác BE của
ABE ACB (c – g - c)
= 8(8 + 10) = 144
AC = 12 cm
Câu 7:
Cho ABC có, Nếu ba cạnh của tam giác trên là ba số tự nhiên liên tiếp thì mỗi cạnh là bao nhiêu?

Thì từ câu a ta có b2 = a(a + c) (1). Vì b > a nên có thể b = a + 1 hoặc b = a + 2
+ Nếu b = a + 1 thì (a + 1)2= a2 + ac 2a + 1 = ac a(c – 2) = 1
a = 1; b = 2; c = 3 (loại)
+ Nếu b = a + 2 thì a(c – 4) = 4
- Với a = 1 thì c = 8 (loại)
- Với a = 2 thì c = 6 (loại)
- Với a = 4 thì c = 6 ; b = 5
Vậy a = 4; b = 5; c = 6
Câu 9:
Cho hình bình hành ABCD. Kẻ . Chứng minh rằng
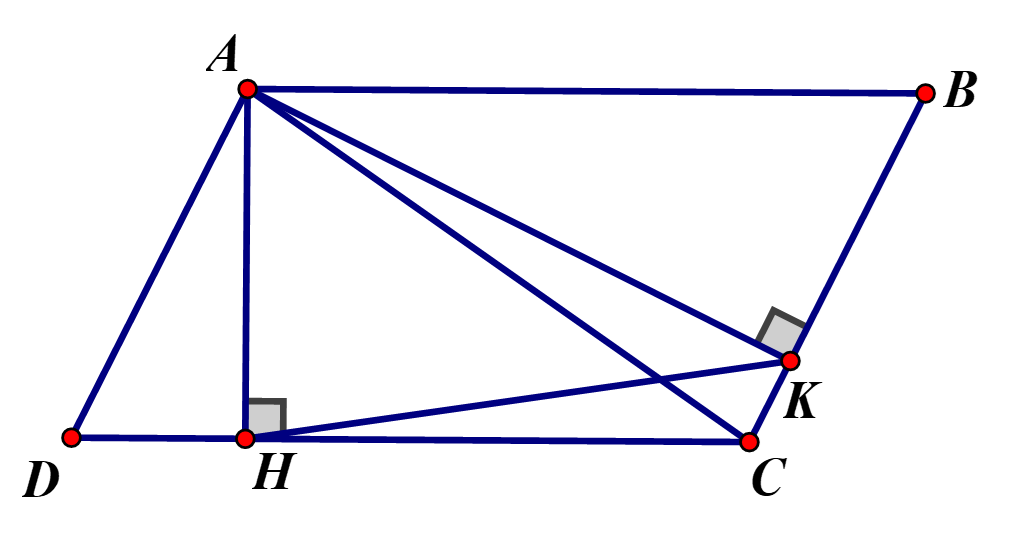
Ta có :
Xét và có
(cùng phụ với )
(chứng minh trên)
(c- g - c)Câu 10:
Ta có (1)
(2)Từ (1) và (2) (3)
Mặt khác nên từ (3) suy ra
Xét và có: ;
(c – g - c)
Câu 11:
Cho hình vuông ABCD. Trên cạnh BC lấy điểm E. Tia AE cắt đường thẳng CD tại M , tia DE cắt đường thẳng AB tại N. Chứng minh rằng
Gọi Olà giao điểm của BM và CN.
Xét có
Câu 12:
Cho vuông tại A có BE là đường phân giác của (). Kẻ cắt BE tại F. Chứng minh
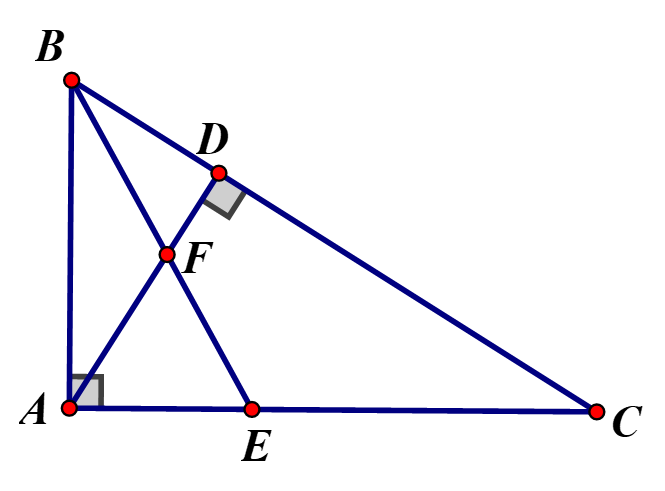
Ta có:BF là đường phân giác của
(1)
BE là đường phân giác của
(2)
Mặt khác (c – g - c)
(3)
Từ (1), (2) và (3) suy raCâu 13:
Cho nhọn, lấy các cạnh và BC dựng các tam giác vuông cân hai tam giác đầu dựng ra phía ngoài , còn tam giác thứ 3 dựng trong cùng một nửa mặt phẳng bờ BC với . Chứng minh rằng tứ giác AEFD là hình bình hành.
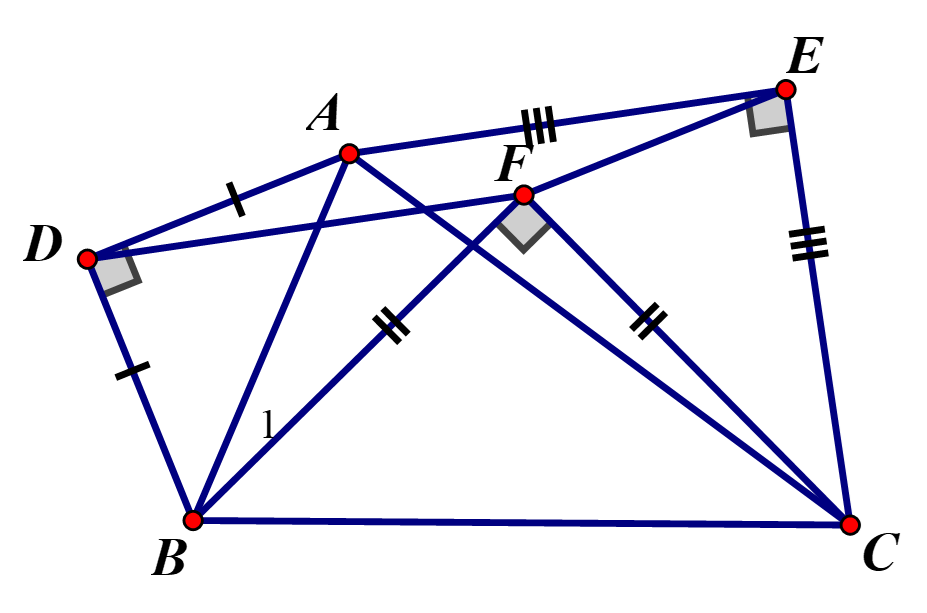
Ta có (Hai tam giác vuông cân)
Mặt khác
(c - g - c)
Chứng minh tương tự ta có
Ta có
Chứng minh tương tự ta được AD // EF. Vậy tứ giác là hình bình hànhCâu 14:
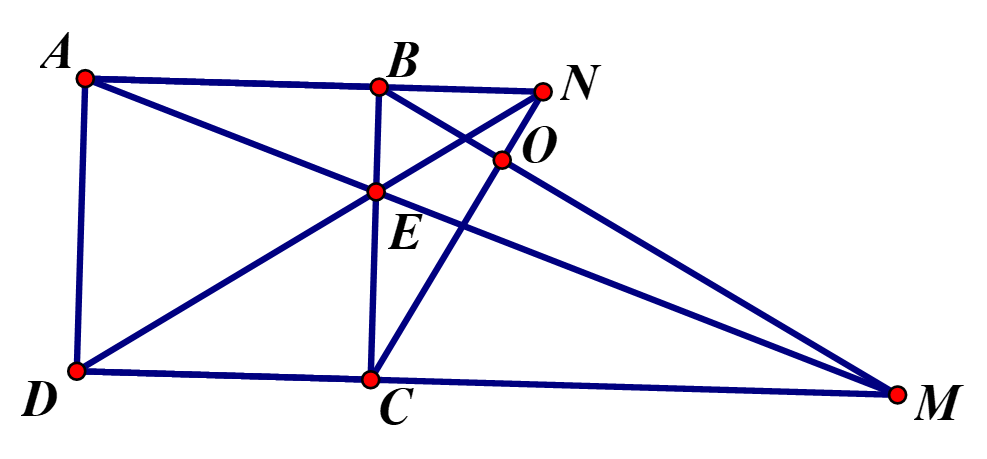
Cho hình thoi ABCD cạnh a có , một đường thẳng bất kỳ qua C cắt tia đối của các tia tại Chứng minh rằng tích có giá trị không đổi
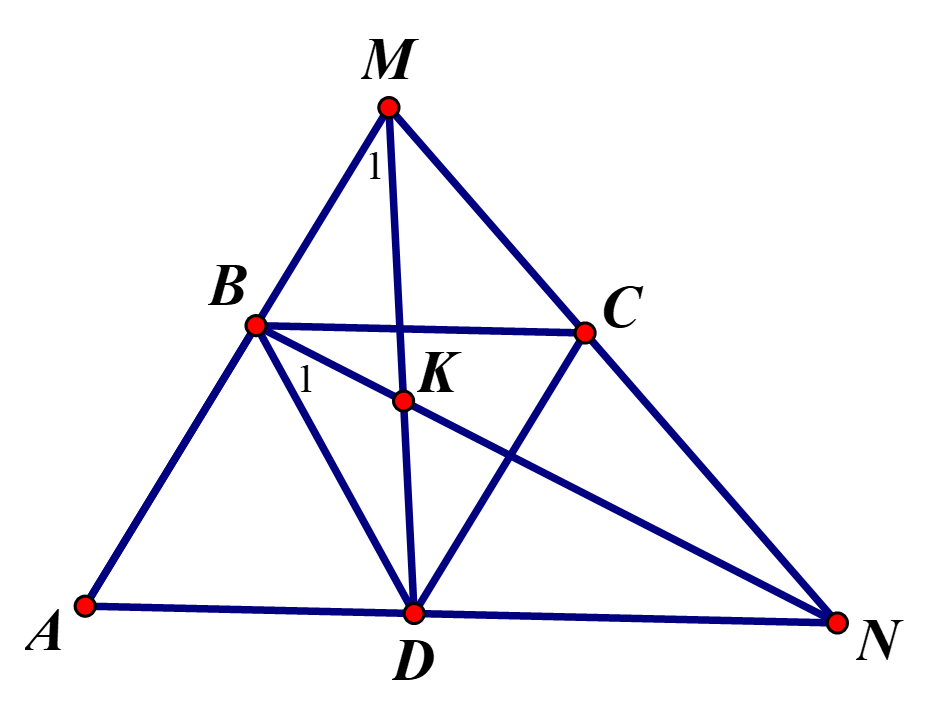
Gọi độ dài cạnh của hình thoi ABCD là a
Ta có (1)
(2)
Từ (1) và (2) suy ra
có giá trị không đổi.Câu 15:
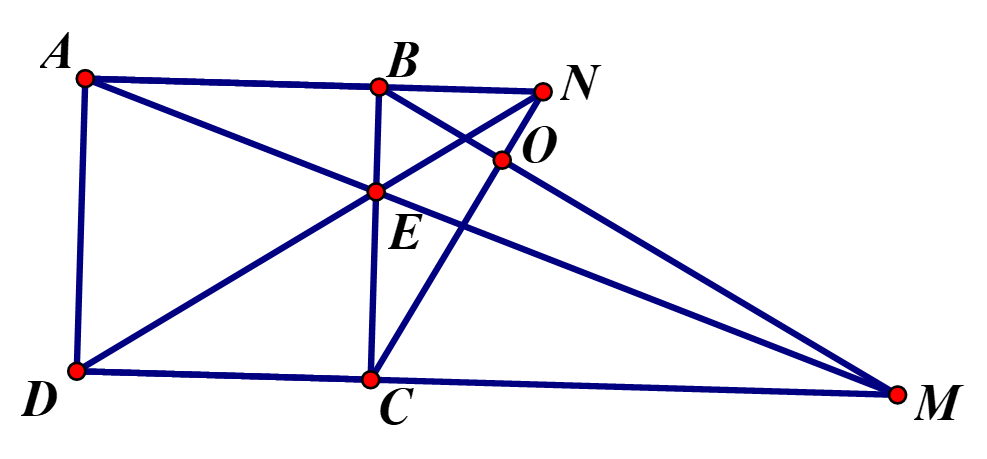
Cho hình thoi ABCD cạnh a có , một đường thẳng bất kỳ qua C cắt tia đối của các tia BA,DA tại M,N. Gọi K là giao điểm của BN và DM. Tính số đo của góc BKD
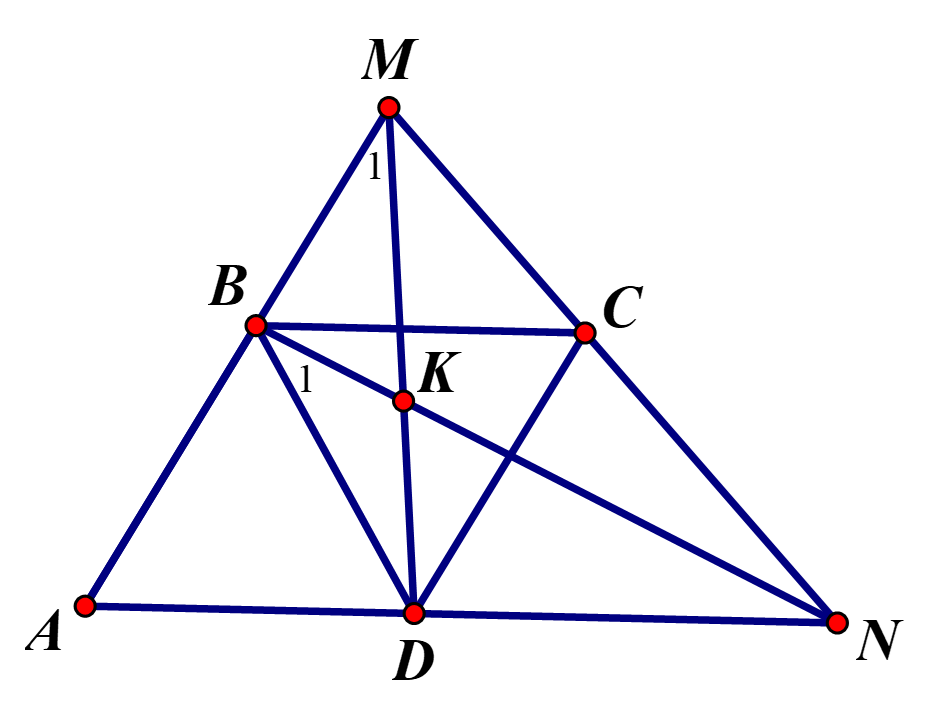
![]() và có
và có
Mặt khác ( Do ABCD là hình thoi có nên)
![]() (c - g - c)
(c - g - c)
Suy ra .
Mặt khác và có và nên