Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Phân tích đa thức thành nhân tử bằng một số phương pháp (có đáp án)
Trắc nghiệm chuyên đề Toán 8 Chủ đề 4: Phân tích đa thức thành nhân tử bằng một số phương pháp (có đáp án)
-
308 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Đa thức 4x( 2y - z ) + 7y( z - 2y ) được phân tích thành nhân tử là ?
Ta có 4x( 2y - z ) + 7y( z - 2y ) = 4x( 2y - z ) - 7y( 2y - z ) = ( 2y - z )( 4x - 7y ).
Chọn đáp án B.
Câu 2:
Đa thức x3( x2 - 1 ) - ( x2 - 1 ) được phân tích thành nhân tử là ?
Ta có x3( x2 - 1 ) - ( x2 - 1 ) = ( x2 - 1 )( x3 - 1 ) = ( x - 1 )( x + 1 )( x - 1 )( x2 + x + 1 )
= ( x - 1 )2( x + 1 )( x2 + x + 1 )
Chọn đáp án D.
Câu 3:
Tìm giá trị y thỏa mãn 49( y - 4 )2 - 9( y + 2 )2 = 0 ?
Ta có 49( y - 4 )2 - 9( y + 2 )2 = 0
⇔ 49( y2 - 8y + 16 ) - 9( y2 + 4y + 4 ) = 0
⇔ 49y2 - 392y + 784 - 9y2 - 36y - 36 = 0
⇔ 40y2 - 428y + 748 = 0 ⇔ 4( 10y2 - 107y + 187 ) = 0
⇔ 4[ ( 10y2 - 22y ) - ( 85y - 187 ) ] = 0 ⇔ 4[ 2y( 5y - 11 ) - 17( 5y - 11 ) ] = 0
⇔ 4( 5y - 11 )( 2y - 17 ) = 0
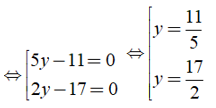
Câu 4:
Ta có A = x2 - y2 + 2y - 1 = x2 - ( y2 - 2y + 1 )
= x2 - ( y - 1 )2 = ( x - y + 1 )( x + y - 1 ) (hằng đẳng thức a2 - b2 = ( a - b )( a + b ) ).
Khi đó với x = 3 và y = 1, ta có A = ( 3 - 1 + 1 )( 3 + 1 - 1 ) = 3.3 = 9.
Chọn đáp án C.
Câu 5:
Phân tích các đa thức sau thành nhân tử
a, ( ab - 1 )2 + ( a + b )2
b, x3 + 2x2 + 2x + 1
c, x2 - 2x - 4y2 - 4y
a) Ta có ( ab - 1 )2 + ( a + b )2 = a2b2 - 2ab + 1 + a2 + 2ab + b2
= a2b2 + a2 + b2 + 1 = ( a2b2 + a2 ) + ( b2 + 1 )
= a2( b2 + 1 ) + ( b2 + 1 ) = ( a2 + 1 )( b2 + 1 )
b) Ta có x3 + 2x2 + 2x + 1 = ( x3 + 1 ) + ( 2x2 + 2x )
= ( x + 1 )( x2 - x + 1 ) + 2x( x + 1 ) = ( x + 1 )( x2 + x + 1 )
c) Ta có x2 - 2x - 4y2 - 4y = ( x2 - 4y2 ) - ( 2x + 4y )
= ( x - 2y )( x + 2y ) - 2( x + 2y )
= ( x + 2y )( x - 2y - 2 ).
Câu 6:
Phân tích các đa thức sau thành nhân tử
b, x3 + 2x2 + 2x + 1
b) Ta có x3 + 2x2 + 2x + 1 = ( x3 + 1 ) + ( 2x2 + 2x )
= ( x + 1 )( x2 - x + 1 ) + 2x( x + 1 ) = ( x + 1 )( x2 + x + 1 )
Câu 7:
Phân tích các đa thức sau thành nhân tử
c, x2 - 2x - 4y2 - 4y
c) Ta có x2 - 2x - 4y2 - 4y = ( x2 - 4y2 ) - ( 2x + 4y )
= ( x - 2y )( x + 2y ) - 2( x + 2y )
= ( x + 2y )( x - 2y - 2 ).
Câu 8:
Tính giá trị của biểu thức sau A = x6 - 2x4 + x3 + x2 - x, biết x3 - x = 6.
Ta có: A = x6 - 2x4 + x3 + x2 - x = ( x6 - 2x4 + x2 ) + ( x3 - x )
= ( x3 - x )2 + ( x3 - x )
Với x3 - x = 6 = ( x3 - x )2 + ( x3 - x ), ta có A = 62 - 6 = 36 - 6 = 30.
Vậy A = 30.
Câu 9:
Tìm x biết
a) x2 - 5x + 6 + ( x - 1 )( x + 2 ) = 0
a) Ta có: x2 - 5x + 6 + ( x - 1 )( x - 2 ) = 0
⇔ [ ( x2 - 2x ) - ( 3x - 6 ) ] + ( x - 1 )( x - 2 ) = 0
⇔ ( x - 2 )( x - 3 ) + ( x - 1 )( x - 2 ) = 0
⇔ ( x - 2 )( 2x - 4 ) = 0
⇔ 2( x - 2 )2 = 0 ⇔ x = 2
Vậy giá trị x cần tìm là x = 2.
Câu 10:
Tìm x biết
b) x3 + x2 - 2 = 0
b) Ta có: x3 + x2 - 2 = 0
⇔ ( x3 - 1 ) + ( x2 - 1 ) = 0
⇔ ( x - 1 )( x2 + x + 1 ) + ( x - 1 )( x + 1 ) = 0
⇔ ( x - 1 )( x2 + x + 1 + x + 1 ) = 0
⇔ ( x - 1 )[ ( x + 1 )2 + 1 ] = 0 ⇔ x = 1 (vì ( x + 1 )2 + 1 ≥ 1 ∀ x )
Vậy giá trị x cần tìm là x = 1.
