Bài tập Toán 8 Chủ đề 1: Tam giác đồng dạng.Định lí Ta-Lét trong tam giác có đáp án
Dạng 5. Bài luyện tập có đáp án
-
625 lượt thi
-
14 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC, các trung tuyến cắt nhau tại G. Tính
Có E là trung điểm của AC (vì BE là trung tuyến) (tính chất trung điểm của đoạn thẳng)
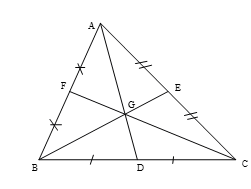
Câu 2:
Cho tam giác ABC, các trung tuyến cắt nhau tại G.Tính
có các trung tuyến cắt nhau tại
G là trọng tâm
(G là trọng tâm )
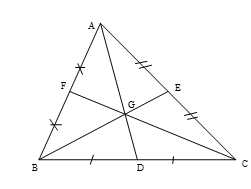
Câu 3:
Cho tam giác ABC, các trung tuyến cắt nhau tại G. Kể hai cặp đoạn thẳng tỉ lệ với AG và GD.
G là trọng tâm
BG và GE là cặp đoạn thẳng tỉ lệ với AG và GD.
CG và GF là cặp đoạn thẳng tỉ lệ với AG và GD.
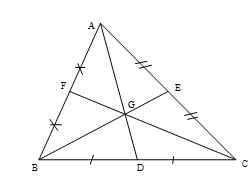
Câu 7:
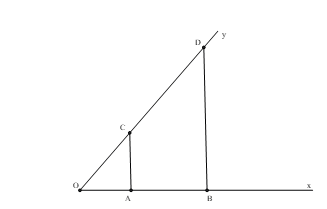
Cho góc . Trên tia Ox, lấy theo thứ tự 2 điểm A,B sao cho Trên tia Oy, lấy điểm C với . Từ B, kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài CD.
Xét có: (gt)
(định lí Ta-let trong tam giác)
Câu 8:
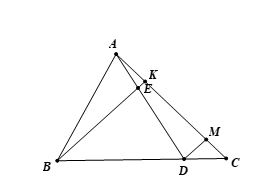
Cho tam giác ACE có Lấy điểm B trên cạnh AC sao cho . Lấy điểm D trên cạnh AE sao cho . Giả sử . Hãy tính: Tỉ số
Theo định lý Ta-lét trong , ta có: .
Câu 9:
Cho tam giác ACE có Lấy điểm B trên cạnh AC sao cho . Lấy điểm D trên cạnh AE sao cho . Giả sử . Hãy tính: Độ dài các đoạn thẳng và AD.
Cách 1. Theo tính chất của tỉ lệ thức ta có:
Từ đó tính được và .
Cách 2. Áp dụng tính chất của dãy tỉ số bằng nhau
Cách 3. Thay vào
Câu 10:
Cho tam giác ABC và điểm D trên cạnh BC sao cho , điểm E trên đoạn AD sao cho . Gọi K là giao điểm của BE và AC. Tính tỉ số .
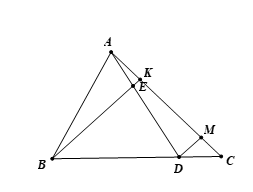
Kẻ
Áp dụng định lý Ta-lét trong , ta có:
(1)
Tương tự với ta có: (2)
Từ (1) và (2), tìm được:
Câu 11:
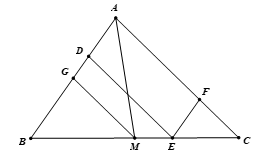
Cho tam giác ABC có AM là trung tuyến và điểm E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC, cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song song với AB, cắt AC ở F. Chứng minh
Chứng minh được ADEF là hình bình hành, từ đó: (1)
Kẻ (G Î AB), ta được G là trung điểm của AB. Áp dụng định lý Ta-lét trong , ta có: (2)
Tương tự với và , ta có:
(3)
Từ (1), (2), (3) ta suy ra
Câu 12:
Cho . Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho Gọi M là giao điểm của DF và BC. Chứng minh
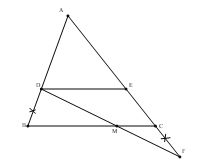
Xét có:
(định lí Ta-let trong tam giác)
Xét có: (vì )
(định lí Ta-let trong tam giác)
Mà (gt)(3) nên từ (1), (2)và (3)
Câu 13:
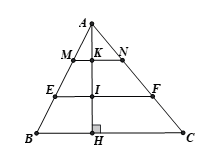
Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I sao cho . Qua I, K lần lượt vẽ các đường thẳng , ( E, M AB, F, N AC). Tính và .
+)
+)
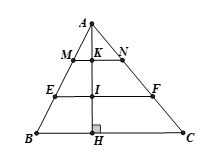
Câu 14:
Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I sao cho . Qua I, K lần lượt vẽ các đường thẳng , ( E, M AB, F, N AC). Cho biết diện tích của tam giác ABC là 90 cm2. Tính diện tích tứ giác MNFE .
có và . Do đó là hình thang có 2 đáy MN, FE, chiều cao KI.