Dạng 3: Vận dụng định lý thuận và định lý đảo của đường trung tuyến ứng với cạnh huyền của tam giác vuông có đáp án
-
963 lượt thi
-
5 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC Chứng minh:
a)
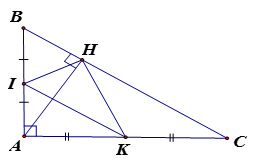
a) Ta có vuông tại H (gt) => IH = IA = IB ( đường trung tuyến ứng với cạnh huyền AB)
cân tại I ( hai góc ở đáy bằng nhau)(1)
Tương tự (2)
Từ (1) và (2) suy ra (gt)
Vậy .
Câu 2:
b) Ta có:
( đường trung tuyến ứng với cạnh huyền trong tam giác vuông AHB) (3)
( đường trung tuyến ứng với cạnh huyền trong tam giác vuông AHC) (4)
( đường trung bình của tam giác ABC) (5)
Từ (3), (4), (5) suy ra: .
Vậy chu vi bằng nửa chu vi
Câu 3:
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
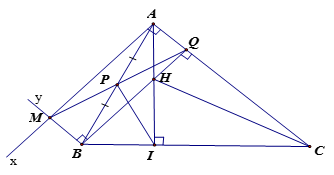
a) Ta có: là hình chữ nhật.
Câu 4:
b) Chứng minh rằng
b) Ta có: là trực tâm của (vì H là giao điểm của hai đường cao)
Suy ra .
Câu 5:
c) Chứng minh tam giác PIQ cân.
c) Ta có:
( vì PQ là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABQ )
( vì PQ là đường trung tuyến ứng với cạnh huyền trong tam giác vuông AIB )
Từ (1) và (2) suy ra PQ = PI => cân tại P.
