Dạng 2. Sử dụng tính chất đối xứng trục để giải toán có đáp án
-
669 lượt thi
-
2 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác vuông ABC ( = 90°). Lấy M bất kì trên cạnh Gọi E, F lần lượt là các điếm đối xứng với M qua AB và AC. Chứng minh: A là trung điểm của EF.
Xem đáp án
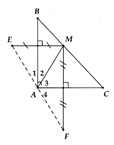

Sử dụng tính chất đối xứng trục Þ AE = AF (=AM) (1).
Sử dụng tính chất của tam giác cân . Từ đó chỉ ra được thằng hàng (2).
Từ (1) và (2) ta có điều phải chứng minh.
Câu 2:
Cho đường thẳng d và hai điểm A, B (như hình vẽ). Tìm vị điểm C trên d để chu vi tam giác ABC nhỏ nhất.

Xem đáp án
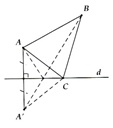

Gọi A' là điểm đối xứng của A qua d => A' cố định.
Vì C Î d => CA = CA' (tính chất đối xứng trục). Ta có:
PABC = AB + AC + BC
= AB + (CA' + CB) AB + BA' (không đổi. Dấu "=" xảy ra tức là chu vi tam giác nhỏ nhất khi C là giao điểm của d và BA'.
