Dạng 4. Tổng hợp có đáp án
-
690 lượt thi
-
18 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình bình hành ABCD. Gọi E là trung điếm của AD, F là trung điểm của BC. Chứng minh:
a) BE = DF và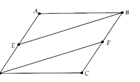
a) Ta chứng minh được BEDF là hình bình hành => BE = DF và .
Cách khác: AEB = CFD (c.g.c) suy ra BE = DF và .
Câu 3:
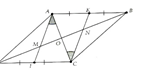
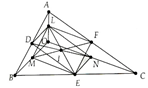
Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của các cạnh AB và CD. Gọi M và N lần lượt là giao điểm của AI và CK với BD. Chứng minh:
a) ADM = CBN;
Câu 5:
c) Từ câu a) => DM= NB. Mặt khác MN = NB (định lý 1 của đường trung bình), từ đó suy ra ĐPCM.
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
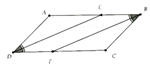
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.
a) Chứng minh DE//BE.
Câu 12:
Cho tam giác ABC. Từ một điểm E trên cạnh AC vẽ đường thẳng song song với BC cắt AB tại F và đường thăng song song vói AB cắt BC tại D. Giả sử AE = BF, chứng minh:
a) Tam giác AED cân;
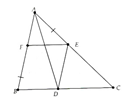
a) Chứng minh BDEF là hình bình hành => ED= BF = AE => AED cân ở E.
Câu 14:
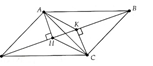
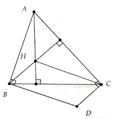
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D.
a) Chứng minh tứ giác BDCH là hình bình hành.
Câu 16:
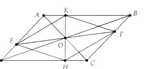
Cho hình bình hành ABCD có AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE cắt BC tại N.
a) Tứ giác MNCD là hình gì?
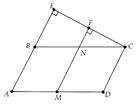
Câu 17:
b) Tam giác EMC là tam giác gì?
b) Chứng minh được F trung điểm CE => EMC cân tại M.
