Dạng 2. Chứng minh tứ giác là hình bình hành có đáp án
-
693 lượt thi
-
5 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của BD, AB, AC, CD
a) Chứng minh rằng EFGH là hình bình hành.
Xem đáp án
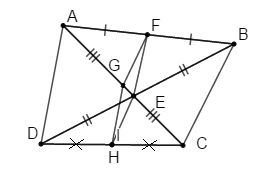 a) Xét có F, E lần lượt là tủng điểm của AB, BD
a) Xét có F, E lần lượt là tủng điểm của AB, BD

=> EF Là đường trung bình của
Tương tự, ta có GH là đường trung bình của
tứ giác GFEH là hình bình hành.
Câu 2:
b) Cho AD = a, BC = b. Tính chu vi của hình bình hành EFGH.
Xem đáp án
b) Ta có:
Tương tự:
=> Chu vi của tứ giác GFEH là: .
Câu 3:
Cho , trực tâm H. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau tại D. CMR:
a) BDCH là hình bình hành.
Xem đáp án


a) Ta có
Lại có ![]()
Từ (1) và (2) => BHCD là hình bình hành.
Câu 5:
c) H, M , D thẳng hàng (M là trung điểm của BC).
Xem đáp án
c) Vì BHCD là hình bình hành nên BC cắt HD tại trung điểm của mỗi đường
ta có: M là trung điểm của BC
=> M là trung điểm của HD
=> H; M; D thẳng hàng.
