Bài tập Toán 8 Chủ đề 9: Tổng ôn các trường hợp đồng dạng của hai tam giác thường có đáp án
Dạng 5: Nhận biết hai tam giác đồng dạng theo trường hợp thứ ba (g.g) để tính độ dài đoạn thẳng có đáp án
-
706 lượt thi
-
6 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:

Gọi là đường phân giác của các góc và thì .
Từ giả thiết theo tỉ số k, suy ra .
Do đó (g.g) theo tỉ số đồng dạng .
Câu 2:
Cho hình bình hành ABCD (hình 303) có . Trên cạnh AB lấy một điểm E sao cho , đường thẳng DE cắt BC ở F .Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng với nhau? Hãy viết các cặp tam giác đồng dạng với nhau theo các đỉnh tương ứng.
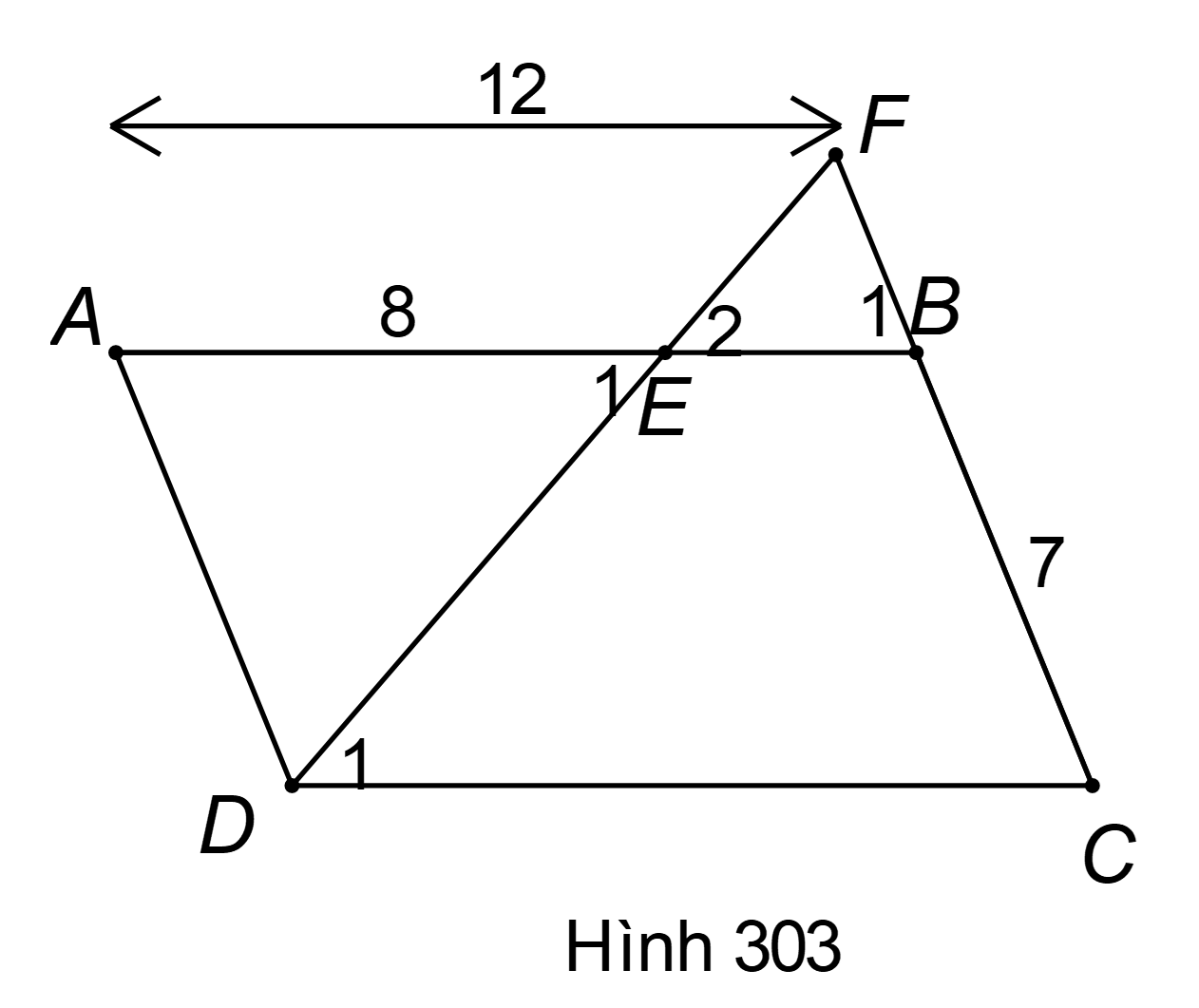
Vì (g.g).
.
(g.g)
Như vậy có tất cả ba cặp tam giác đồng dạng như trên.
Câu 3:
Cho hình bình hành ABCD (hình 303) có . Trên cạnh AB lấy một điểm E sao cho , đường thẳng DE cắt BC ở F. Tính độ dài các đoạn thẳng EF và BF, biết rằng .
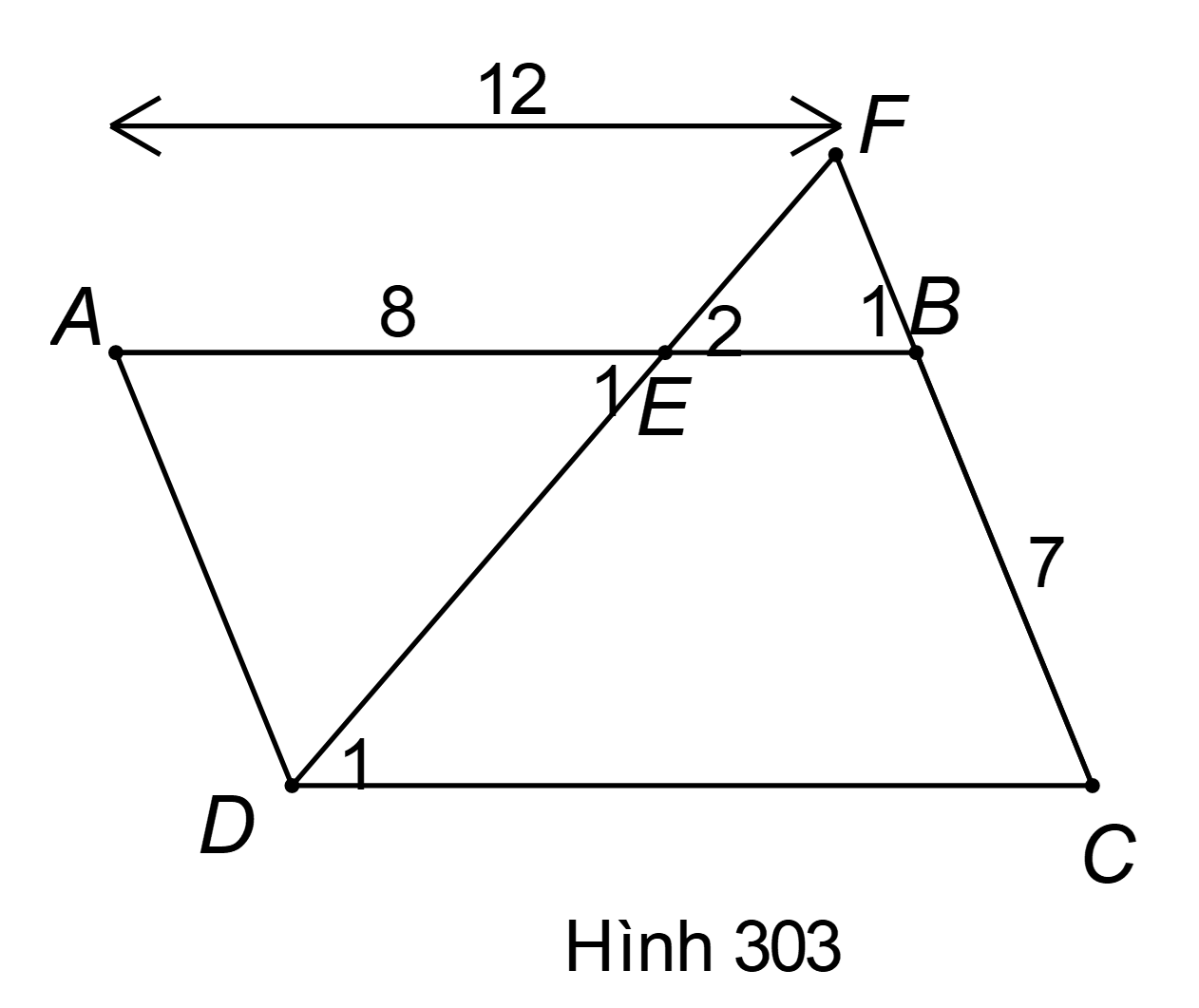
Từ câu a) hay
.
Câu 4:
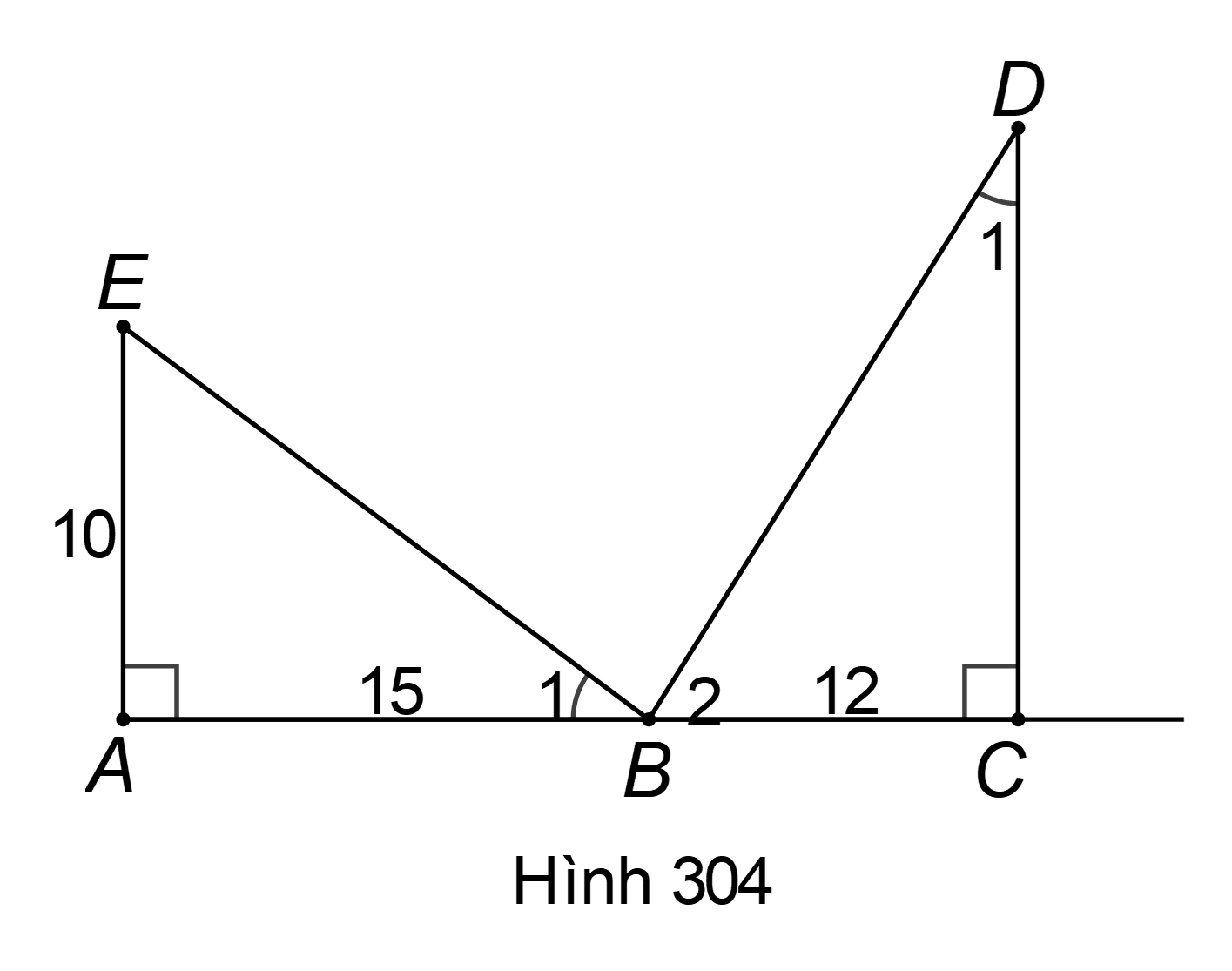
Hình 304 cho biết .Trong hình vẽ có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.
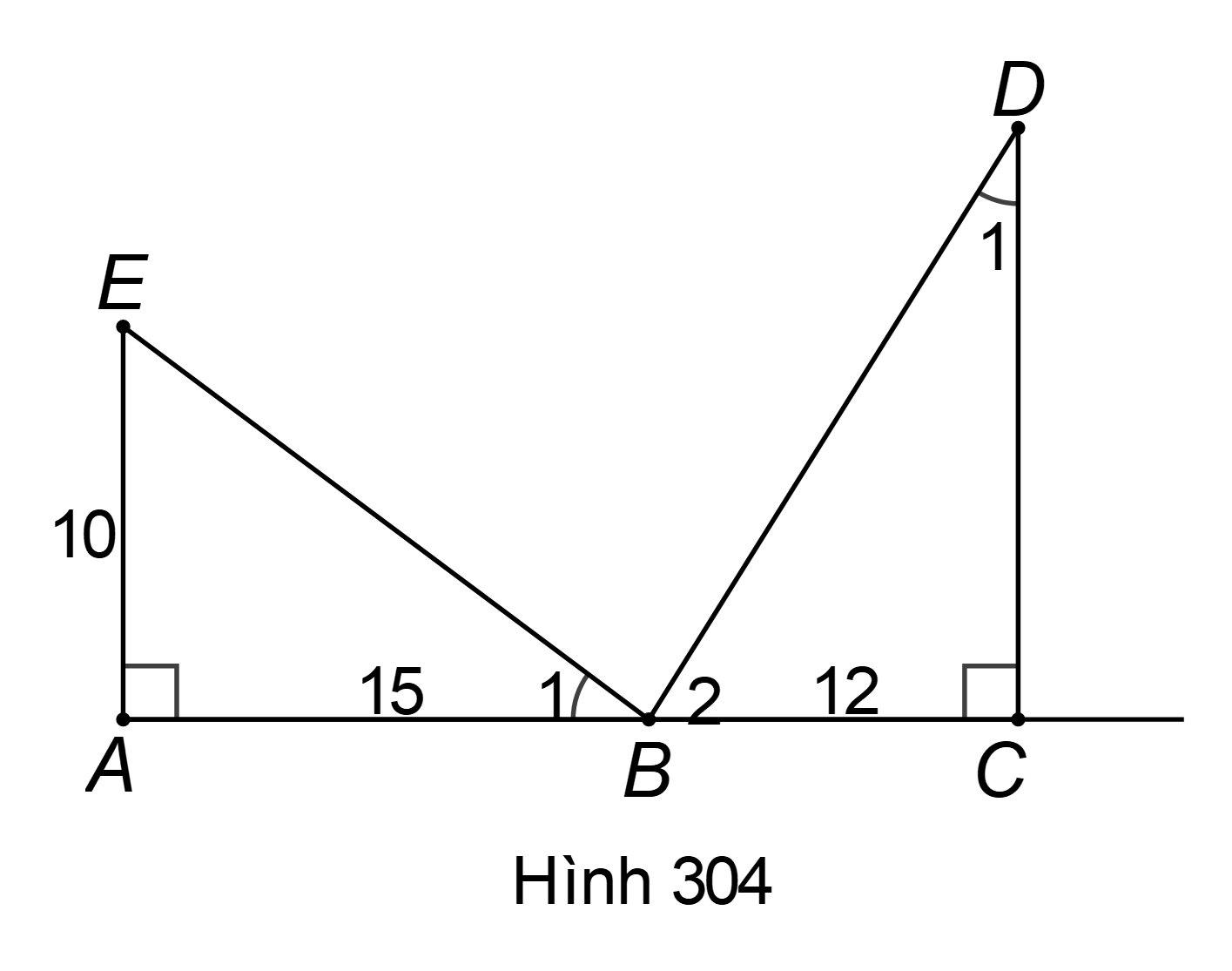
Từ giả thiết và tính chất về góc của tam giác vuông BCD, ta có: , do là góc bẹt.
Vậy trong hình vẽ có ba tam giác vuông là và .
Câu 5:
Hình 304 cho biết .Trong hình vẽ có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó. Cho biết . Hãy tính độ dài các đoạn thẳng và ED (làm tròn đến chữ số thập phân thứ nhất).
Vì (g.g)
Suy ra hay .
Áp dụng định lý Py-ta-go vào tam giác vuông ở A, ta được:
hay .
Áp dụng định lí Py-ta-go vào tam giác BCD vuông ở C, ta được:
hay .
Áp dụng định lí Py-ta-go vào tam giác EBD vuông ở B, ta được:
hay .