9 câu hỏi trắc nghiệm thuộc Đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)_ đề 6

Câu 1:

Số dư khi chia đa thức x² + 2x + 3 cho đa thức x + 1 là:

A. – 2

B. 1

C. 2

D. 0

Xem đáp án

1. C

Câu 2:

Khẳng định nào sau đây là sai?

A. Hình thang có hai cạnh bên bằng nhau là hình thang cân.

B. Hai tam giác bằng nhau có diện tích bằng nhau

C. Tứ giác có các cạnh đối song song là hình bình hành.

D. Hình thoi có một góc vuông là hình vuông.

Xem đáp án

2. A

Câu 3:

Kết quả của phép tính $\frac{x^{2} - 6 x + 9}{x + 2} : \frac{x - 3}{2 x + 4}$ là:

A. 2x – 6

B. x – 3

C.

\frac{x - 3}{2}

D. 6 – 2x

Xem đáp án

3. A

Câu 4:

Giá trị của phân thức $\frac{3 x - 5}{2 x + 8}$ được xác định khi:

A.

x \neq 4

B.

x \neq \frac{5}{3}

C.

x \neq - 4

D.

x \neq - \frac{5}{3}

Xem đáp án

4. C

Câu 5:

Hình nào dưới đây không có trục đối xứng:

A. Hình thoi

B. Hình vuông

C. Hình chữ nhật

D. Hình bình hành

Xem đáp án

5. D

Câu 6:

Giá trị lớn nhất của $B = \frac{2}{x^{2} - 2 x + 5}$ là:

A. 2

B.

\frac{2}{5}

C. 4

D.

\frac{1}{2}

Xem đáp án

6. D

Câu 7:

Cho biểu thức $A = (\frac{2 x}{x + 1} + \frac{x - 1}{x} - \frac{3 x^{2} - 2 x - 1}{x^{2} + x}) : (\frac{- x + 5}{x - 3} + 1)$

a) Tìm điều kiện xác định của A. Chứng tỏ $A = \frac{x - 3}{x + 1}$ .

b) Tính giá trị của A biết |x + 2| = 1.

c) Tìm x để $A = \frac{1}{2} .$

Xem đáp án

a) Điều kiện xác định:

x^{2} + x \neq 0 \Leftrightarrow x (x + 1) \neq 0 \Leftrightarrow {\begin{cases} x \neq 0 \\ x + 1 \neq 0 \end{cases} \Leftrightarrow {\begin{cases} x \neq 0 \\ x \neq - 1 \end{cases}

.

A = (\frac{2 x}{x + 1} + \frac{x - 1}{x} - \frac{3 x^{2} - 2 x - 1}{x^{2} + x}) : (\frac{- x + 5}{x - 3} + 1)

A = (\frac{2 x^{2}}{x (x + 1)} + \frac{(x - 1) (x + 1)}{x (x + 1)} - \frac{3 x^{2} - 2 x - 1}{x (x + 1)}) : (\frac{- x + 5}{x - 3} + \frac{x - 3}{x - 3})

A = (\frac{2 x^{2} + x^{2} - 1 - 3 x^{2} + 2 x + 1}{x (x + 1)}) : (\frac{- x + 5 + x - 3}{x - 3})

A = \frac{2 x}{x (x + 1)} : \frac{2}{x - 3}

A = \frac{2 x}{x (x + 1)} . \frac{x - 3}{2}

A = \frac{x - 3}{x + 1} .

b) Ta có |x + 2| = 1 $\Leftrightarrow [\begin{array}{l} x + 2 = 1 \\ x + 2 = - 1 \end{array} \Leftrightarrow [\begin{array}{l} x = - 1 (K T M) \\ x = - 3 (T M) \end{array}$

Thay x = -3 (TMĐK) vào A, ta được:

$A = \frac{- 3 - 3}{- 3 + 1} = \frac{- 6}{- 2} = 3.$

c) Xét $A = \frac{1}{2}$

$\Leftrightarrow \frac{x - 3}{x + 1} = \frac{1}{2}$

$\Leftrightarrow 2 (x - 3) = x + 1$

$\Leftrightarrow 2 x - 6 = x + 1$

$\Leftrightarrow 2 x - x = 1 + 6$

\Leftrightarrow x = 7.

Câu 8:

Tìm x, biết:

a) $5 x (x - 3) - x^{2} + 9 = 0$

b) $x + 4 x^{2} + 4 x^{3} = 0$

c) $\frac{x^{2} - 4}{(x + 1) (x - 2)} = 0$

Xem đáp án

a) $5 x (x - 3) - x^{2} + 9 = 0$

$\Leftrightarrow 5 x (x - 3) - (x^{2} - 9) = 0$

$\Leftrightarrow 5 x (x - 3) - (x - 3) (x + 3) = 0$

$\Leftrightarrow (x - 3) (5 x - x - 3) = 0$

$\Leftrightarrow (x - 3) (4 x - 3) = 0$

$\Leftrightarrow [\begin{array}{l} x - 3 = 0 \\ 4 x - 3 = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 3 \\ x = \frac{3}{4} \end{array}$

Vậy

x \in {3; \frac{3}{4}} .

b) $x + 4 x^{2} + 4 x^{3} = 0$

$\Leftrightarrow x (1 + 4 x + 4 x^{2}) = 0$

$\Leftrightarrow x (4 x^{2} + 4 x + 1) = 0$

$\Leftrightarrow x {(2 x + 1)}^{2} = 0$

$\Leftrightarrow [\begin{array}{l} x = 0 \\ {(2 x + 1)}^{2} = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = 0 \\ 2 x + 1 = 0 \end{array}$

\Leftrightarrow [\begin{array}{l} x = 0 \\ x = - \frac{1}{2} \end{array}

Vậy

x \in {- \frac{1}{2}; 0} .

c) $\frac{x^{2} - 4}{(x + 1) (x - 2)} = 0$

Điều kiện xác định:

$(x + 1) (x - 2) \neq 0 \Leftrightarrow {\begin{cases} x + 1 \neq 0 \\ x - 2 \neq 0 \end{cases} \Leftrightarrow {\begin{cases} x \neq - 1 \\ x \neq 2 \end{cases}$

$\frac{x^{2} - 4}{(x + 1) (x - 2)} = 0$

$\Leftrightarrow \frac{(x - 2) (x + 2)}{(x + 1) (x - 2)} = 0$

$\Leftrightarrow \frac{x + 2}{x + 1} = 0$

$\Leftrightarrow x + 2 = 0$

$\Leftrightarrow x = - 2$ (TMĐK)

Vậy x = -2.

Câu 9:

Cho tam giác ABC cân tại A, đường cao AD, O là trung điểm của AC, điểm E đối xứng với điểm D qua điểm O.

a) Chứng minh tứ giác AECD là hình chữ nhật.

b) Gọi I là trung điểm của AD, chứng tỏ I là trung điểm của BE.

c) Cho AB = 10 cm, BC = 12 cm. Tính diện tích tam giác OAD.

d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để tứ giác AEDK là hình thang cân.

Xem đáp án

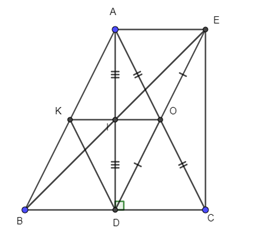
a) Xét tứ giác AECD, có:

Hai đường chéo AC và DE cắt nhau tại O

O là trung điểm của AC (gt)

O là trung điểm của DE (E đối xứng với D qua O)

Suy ra tứ giác AECD là hình bình hành.

Ta lại có $A D ⊥ B C \Rightarrow \hat{A D C} = 90^{0}$

\Rightarrow

AECD là hình chữ nhật.

b) Vì AECD là hình chữ nhật nên AD = CD và AD // CD hay AD // BD.

Xét $Δ A B C$ cân tại A, có AD là đường cao nên AD cũng là đường là đường trung tuyến

$\Rightarrow$ D là trung điểm của BC.

$\Rightarrow$ BD = DC

Mà AD = DC

$\Rightarrow$ AD = DB

Xét ABDE có AD = DB và AD // BD nên ABDE là hình bình hành

Mặt khác I là trung điểm AD

Do đó I là trung điểm của BE.

c) Ta có: $B D = D C = \frac{B C}{2} = \frac{12}{2} = 6 c m$ (D là trung điểm của BC)

Xét tam giác ADC có:

O là trung điểm AC

I là trung điểm của AD

$\Rightarrow$ OI là đường trung bình tam giác ADC

$\Rightarrow$ OI // DC và $O I = \frac{1}{2} D C = \frac{1}{2} .6 = 3 c m$ .

Mà $D C ⊥ A D$ (gt)

$\Rightarrow O I ⊥ A D$

Xét $Δ A B D$ vuông tại D, có:

AB² = AD² + DB² (định lý Py – ta – go)

10² = AD² + 6²

100 = AD² + 36

AD² = 100 – 36

AD² = 64

AD = 8 cm.

Diện tích tam giác OAD là:

S_{O A D} = \frac{1}{2} . A D . O I = \frac{1}{2} .8.3 = 12 (c m^{2}) .

d) Ta có ABDE là hình bình hành nên AB // DE hay AK // DE

Suy ra AKDE là hình thang.

Nên để AKDE là hình thang cân thì $\hat{A E D} = \hat{K D E}$ (hai góc kề một đáy bằng nhau)

Mà $\hat{A E D} = \hat{A B D}$ (hai góc đối trong hình bình hành ABDE)

Tứ giác AODK có hình bình hành nên $\hat{K A O} = \hat{K D E}$

$\Rightarrow \hat{K A O} = \hat{A B C}$

$\Rightarrow Δ A B C$ đều.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)

Đề kiểm tra Học kì 1 Toán 8 có đáp án (Mới nhất)_ đề 6

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương