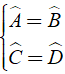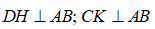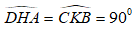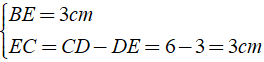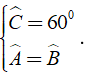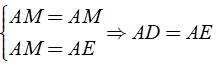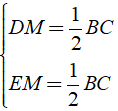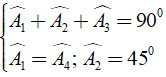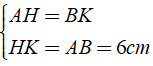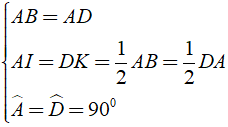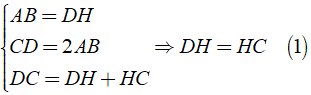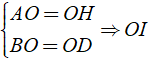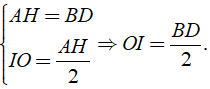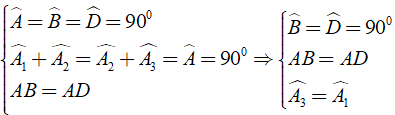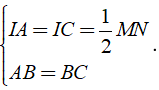Tổng hợp Lý thuyết & Trắc nghiệm Chương 1 Hình học 8
-
1167 lượt thi
-
70 câu hỏi
-
100 phút
Danh sách câu hỏi
Câu 2:
Số đo các góc của tứ giác ABCD theo tỷ lệ A:B:C:D = 4:3:2:1. Số đo các góc theo thứ tự đó là?
Câu 10:
Điền cụm từ thích hợp vào chỗ trống
A. Hình thang cân là…………………………………..
B. Hình thang có………………. là hình thang cân
C. Hai cạnh bên của hình thang cân…………………..
D. Hình thang cân có hai góc kề một đáy…………….
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
→ Đáp án A điền: “hình thang có hai góc kề một đáy bằng nhau”.
+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
→ Đáp án B điền: “hai góc kề một đáy bằng nhau”
+ Hai cạnh bên của hình thang cân bằng nhau.
→ Đáp án C điền: “bằng nhau”
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau
→ Đáp án D điền: “bằng nhau”
Câu 11:
Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:
A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
B. Hình thang cân có hai cạnh bên bằng nhau.
C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.
D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
→ Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.
+ Hình thang cân có hai cạnh bên bằng nhau.
→ Đáp án B đúng.
+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
→ Đáp án D đúng, đáp án C sai.
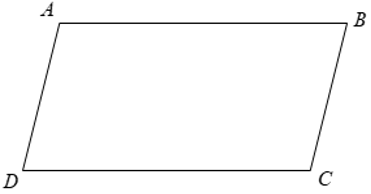
Câu 12:
Cho hình thang cân ABCD (như hình vẽ) có . Số đo của
Áp dụng tính chất của hình thang cân ta có:
Câu 13:
Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC. Phát biểu nào sau đây sai?
Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC
⇒ DE là đương trung bình của tam giác ABC
Hay DE//BC và DE = 1/2BC.
+ Hình thang cân là hình thang có hai góc kề một cạnh bằng nhau và hai cạnh bên bằng nhau nhưng bài toán này hai góc kề một cạnh đấy không bằng nhau
→ Đáp án C sai.
Chọn đáp án C.
Câu 14:
Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC và DE = 4cm. Biết đường cao AH = 6cm. Diện tích của tam giác ABC là?
Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC
⇒ DE là đương trung bình của tam giác ABC
Hay DE//BC và DE = 1/2BC ⇒ BC = 2DE = 2.4 = 8( cm )
Khi đó ta có: S = 1/2AH.BC = 1/2.6.8 = 24
Chọn đáp án A.
Câu 15:
Chọn phát biểu đúng
Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
→ Đáp án A đúng.
+ Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng của hai đáy.
+ Một hình thang thì chỉ có 1 đường trung bình duy nhất.
Chọn đáp án A.
Câu 16:
Với a, b, h lần lượt là độ dài đáy lớn, đáy nhỏ và chiều cao của hình thang thì công thức diện tích của hình thang là ?
Diện tích hình thang bằng nửa tổng độ dài hai đáy nhân với đường cao của hình thang,
⇒ S = 1/2( a + b )h
Chọn đáp án B.
Câu 17:
Chọn phương án đúng nhất trong các phương án sau
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Chọn đáp án C.
Câu 18:
Cho đoạn thẳng AB có độ dài là 3cm và đường thẳng d, đoạn thẳng A'B' đối xứng với AB qua d, khi đó độ dài của A'B' là ?
Tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Khi đó AB = A'B' = 3cm.
Chọn đáp án A.
Câu 19:
Tam giác ABC đối xứng với tam giác A'B'C' qua đường thẳng d, biết chu vi của tam giác ABC là 48cm thì chu vi của tam giác A'B'C' là ?
Tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Khi đó ta có:
Chọn đáp án D.
Câu 20:
Chọn phương án sai trong các phương án sau?
Dấu hiệu nhận biết hình bình hành.
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
⇒ Đáp án C sai.
Chọn đáp án C.
Câu 21:
Chọn phương án đúng trong các phương án sau.
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
⇒ Đáp án C đúng.
Chọn đáp án C.
Câu 23:
Cho hình bình hành ABCD có . Kẻ Tìm khẳng định sai?
* Ta có:
nên DH // CK.
Vì ABCD là hình bình hành nên AB // CD hay HK// CD.
Xét tứ giác HKCD có: DH// CK và HK// CD nên tứ giác HKCD là hình bình hành.
* Xét ΔDHA và ΔCKB có:
DH = CK (vì HKCD là hình bình hành)
AD = BC (vì ABCD là hình bình hành)
Suy ra: ΔDHA = ΔCKB (c.g.c)
Suy ra: HA = KB ( 2 cạnh tương ứng)
Chọn đáp án B
Câu 24:
Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
Trong hình bình hành các góc đối bằng nhau
Hay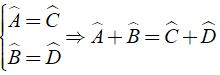
+ Δ ABD cân tại A khi và chỉ khi AB = AD nhưng theo giả thiết ta chưa có dữ kiện này
→ Đáp án B sai.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
→ Đáp án A sai vì theo giả thiết chữ đủ dữ kiện
Chọn đáp án C.
Câu 25:
Chọn đáp án đúng trong các đáp án sau
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Chọn đáp án C.
Câu 26:
Cho AB = 6cm, A' là điểm đối xứng với A qua B, AA' có độ dài bằng bao nhiêu ?
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Khi đó, A' là điểm đối xứng với A qua B thì AB = BA' = 6cm
⇒ AA' = AB + BA' = 6 + 6 = 12cm
Chọn đáp án B.
Câu 27:
Chọn phương án sai trong các phương án sau đây
Ta có tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
Các phương án đúng là:
+ Đáp án A: Hai đoạn thẳng đối xứng với nhau qua một điểm thì chúng bằng nhau.
+ Đáp án B: Hai góc đối xứng với nhau qua một điểm thì chúng bằng nhau.
+ Đáp án D: Hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.
→ Đáp án C sai.
Chọn đáp án C.
Câu 28:
Hình nào dưới đây có tâm không phải là giao điểm của hai đường chéo?
Các hình có tâm đối xứng là giao điểm điểm của hai đường chéo là
+ Hình bình hành
+ Hình chữ nhật
+ Hình thoi
→ Hình thang không có tâm đối xứng là giao điểm của hai đường chéo.
Chọn đáp án D.
Câu 29:
Cho tam giác ABC và tam giác A'B'C' đối xứng với nhau qua điểm I biết AB = 4cm, AC = 8cm và chu vi của tam giác ABC bằng 22cm. Hỏi độ dài cạnh B'C' của tam giác A'B'C' là?
Ta có tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
Khi đó ta có: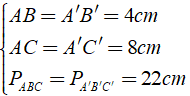
Chọn đáp án D.
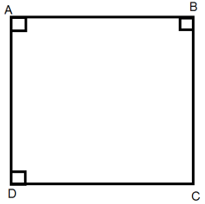
Câu 30:
Chọn đáp án đúng nhất trong các đáp án sau?
Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.
Chọn đáp án B.
Câu 31:
Tìm câu sai trong các câu sau
Định lý trong hình chữ nhật
+ Hình chữ nhật có hai đường chéo bằng nhau.
+ Hình chữ nhật có hai đường chéo cắt nhau tại trung điểm tại trung điểm mỗi đường.
+ Giao của hình đường chéo của hình chữ nhật là tâm của hình chữ nhật đó.
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
→ Đáp án C sai.
Chọn đáp án C.
Câu 32:
Các dấu hiệu nhận biết sau, dấu hiệu nào nhận biết chưa đúng?
Dấu hiệu nhận biết hình chữ nhật:
+ Tứ giác có ba góc vuông là hình chữ nhật.
+ Hình thang cân có một góc vuông là hình chữ nhật.
+ Hình bình hành có một góc vuông là hình chữ nhật.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
⇒ Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường chưa đủ điều kiện để là hình chữ nhật.
Chọn đáp án A.
Câu 33:
Khoanh tròn vào phương án sai
Định lý
+ Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
⇒ Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì vuông góc với cạnh huyền nếu tam giác vuông đó là tam giác vuông cân.
Chọn đáp án D.
Câu 34:
Trong hình chữ nhật có kích thước lần lượt là 5cm và 12cm. Độ dài đường chéo của hình chữ nhật là?
Độ dài của đường chéo hình chữ nhật bằng căn bậc hai tổng hai bình phương của hai kích thước hình chữ nhật
Do đó, độ dài đường chéo là
Chọn đáp án B.
Câu 35:
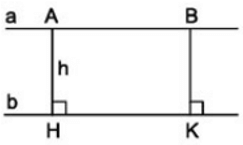
Chọn phương án đúng nhất trong các phương án sau?
Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia. h là khoảng cách giữa hai đường thẳng song song a và b.
Chọn đáp án C.
Câu 36:
Chọn phương án đúng trong các phương án sau
Tính chất:
Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng song song với b và cách b một khoảng bằng h.
Nhận xét: Từ định nghĩa về khoảng cách hai đường thẳng song song và tính chất trên ta có: Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
Chọn đáp án B.
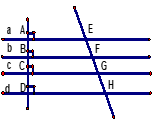
Câu 37:
Cho hình sau trong đó các đường thẳng a,b,c,d song song với nhau. Nếu các đường thẳng a,b,c,d song song cách đều thì :
Định lí:
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
Chọn đáp án C.
Câu 38:
Khoanh tròn vào phương án đúng trong các phương án sau ?
Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.
Chọn đáp án D.
Câu 39:
Trong các khẳng định sau, khẳng định nào sai về hình thoi ?
Định lí: Trong hình thoi:
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác các góc của hình thoi.
+ Hai đường chéo cắt nhau tại trung điểm mỗi đường.
⇒ Đáp án A sai.
Chọn đáp án A.
Câu 41:
Hình thoi có độ dài các cạnh là 4cm thì chu vi của hình thoi là ?
Chu vi của hình thoi là
Chọn đáp án C.
Câu 42:
Các phương án sau, phương án nào sai?
Định lí:
+ Hai thoi có hai trực đối xứng là hai đường chéo của hình thoi.
+ Có một tâm đối xứng là giao điểm của hai đường chéo.
Mở rộng:
+ Trong hình chữ nhật, các trung điểm của các cạnh hĩnh chữ nhật là các đỉnh của một hình thoi.
+ Trong hình thoi, các trung điểm của bốn cạnh hình thoi là các hình chữ nhật.
⇒ Đáp án D sai.
Chọn đáp án D.
Câu 43:
Hãy khoan tròn vào phương án đúng nhất trong các phương án sau ?
+ Tứ giác có 4 góc vuông là hình chữ nhật
Hình chữ nhật có 4 cạnh bằng nhau là hình vuông.
⇒ Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
Chọn đáp án A.
Câu 44:
Hãy chọn đáp án sai trong các phương án sau đây ?
+ Trong hình vuông có hai đường chéo vuông góc với nhau, bằng nhau và cắt nhau tại trung điểm mỗi đường
+ Hai đường chéo trong hình vuông đồng thời là trục đối xứng của hình vuông đó.
⇒ Đáp án B sai.
Chọn đáp án B.
Câu 45:
Trong các dấu hiệu nhận biết sau thì dấu hiệu nào không đủ điều kiện để tứ giác là hình vuông?
Dấu hiệu nhận biết hình vuông:
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
⇒ Hình bình hành có hai đường chéo bằng nhau thì không là hình vuông.
⇒ Đáp án D sai.
Chọn đáp án D.
Câu 46:
Tìm câu nói đúng khi nói về hình vuông?
Dấu hiệu nhận biết hình vuông:
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
⇒ Hình vuông vừa là hình chữ nhật, cũng vừa là hình thoi.
⇒ Cả 3 phương án đều đúng.
Chọn đáp án D.
Câu 47:
Một hình vuông có độ dài cạnh bằng 4cm thì độ dài đường chéo của hình vuông là ?
Hình vuông có độ dài cạnh là a( cm )
Áp dụng định lý Py – to – go thì độ dài đường chéo của hình vuông là
Do đó với a = 4 thì độ dài đường chéo là
Chọn đáp án B.
Câu 50:
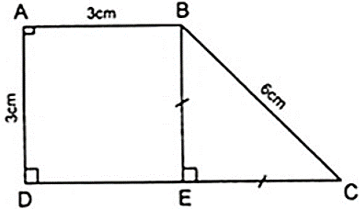
Hình thang vuông ABCD có ; AB = AD = 3cm; CD = 6cm. Tính số đo góc B và C của hình thang ?
Kẻ BE ⊥ CD thì AD//BE do cùng vuông góc với CD
+ Hình thang ABED có cặp cạnh bên song song là hình bình hành.
Áp dụng tính chất của hình bình hành ta có
AD = BE = 3cm.
Xét Δ BEC vuông tại E có
⇒ Δ BEC là tam giác vuông cân tại E.
Câu 51:
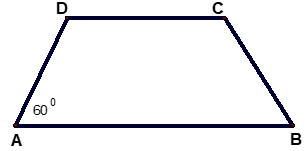
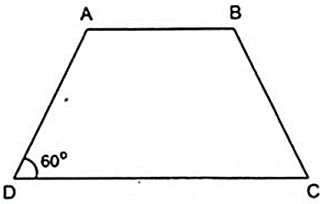
Hình thang vuông ABCD có ; AB = AD = 3cm; CD = 6cm. Tính các góc của hình thang cân, biết có một góc bằng 60 độ
Xét hình thang cân ABCD ( AB//CD ) có Dˆ = 600
Theo định nghĩa và giả thiết về hình thang cân ta có:
Do góc A và góc D là hai góc cùng nằm một phía của
Câu 52:
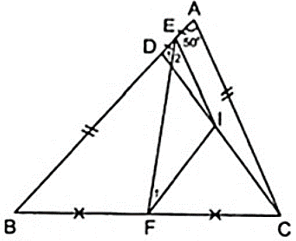
Cho tam giác ABC ( AB > AC ) có . Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E,F lần lượt là trung điểm của cạnh AD,BC. Tính
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác BCD và ACD.
Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
( 1 ) FI//BD ( 2 ) FI = a
( 3 ) EI = a ( 4 ) EI//AC
Câu 54:
Chứng minh rằng các đường cao của hình thoi bằng nhau
Xét hình thoi ABCD, kẻ hai đường cao AH ⊥ BC, AK ⊥ CD
Ta cần chứng minh: AH = AK.
Áp dụng định nghĩa, tính chất về góc và giả thiết của hình thoi ABCD, ta có:
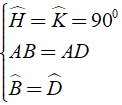
⇒ AH = AK (cặp cạnh tương ứng bằng nhau)
→ (đpcm)
Câu 55:
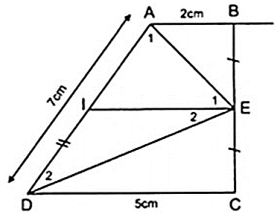
Cho hình thang ABCD ( AB//CD ) có AB = 2cm, CD = 5cm, AD = 7cm. Gọi E là trung điểm của BC. Tính
Do E là trung điểm của BC theo giả thiết vẽ I là trung điểm của AD thì
AI = ID = AD/2 = 3,5( cm ). ( 1 )
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có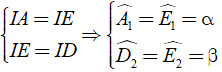
+ Xét tam giác ADE có
Câu 56:
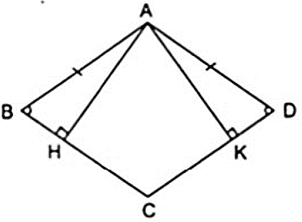
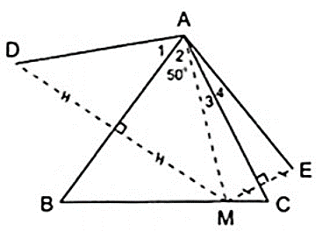
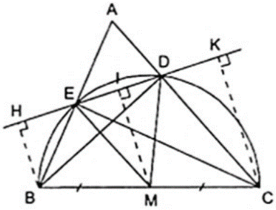
Cho Δ ABC có , điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC. Chứng minh rằng AD = AE.
Theo giả thiết ta có:
+ D đối xứng với M qua AB.
+ E đối xứng với M qua AC.
+ A đối xứng với A qua AB, AC.
AD đối xứng với AM qua AB, AE đối xứng với AM qua AC.
⇒ Áp dụng tính chất đối xứng ta có:
⇒ (đpcm).
Câu 58:
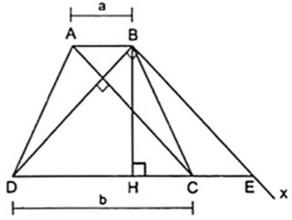
Cho tam giác nhọn ABC, các đường cao BD, CE. Gọi H, K lần lượt là các chân đường cao kẻ từ kẻ từ B và C đến đường thẳng DE. Chứng minh rằng HE = DK.
Vì BD, CE là đường cao của tam giác ABC nên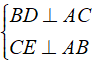
Gọi M là trung điểm của BC
⇒ DM, EM là đường trung tuyến ứng với cạnh huyền của Δ BDC và Δ CEB.
Áp dụng tính chất của đường trung tuyến ứng với cạnh huyền của hai tam giác trên ta được:
⇒ DM = EM ⇒ Δ MDE cân tại M.
Từ giả thiết ta có tứ giác BHKC là hình thang vuông nên vẽ MI ⊥ DE thì BH//MI//CK ( 1 ) (vì cùng vuông góc với đường thẳng DE)
Mà ta có BM = MC ( 2 ) (do ta vẽ hình trên)
Từ ( 1 ),( 2 ) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK ( 3 ).
Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được:
EI = ID ( 4 ).
Trừ theo vế đẳng thức ( 3 ) cho ( 4 ), ta được: HE = DK.
Câu 59:
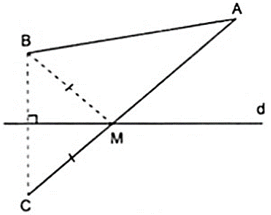
Cho hai điểm A, B cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên d điểm M sao cho tổng MA + MB nhỏ nhất.
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d
Câu 60:
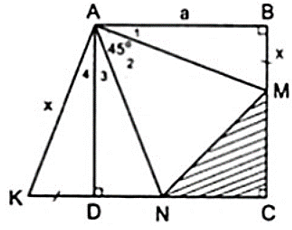
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính : Tính số đo
Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
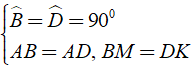
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
Câu 61:
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính : Chu vi tam giác MCN theo a.
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
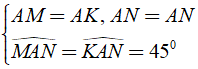
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.
Câu 62:
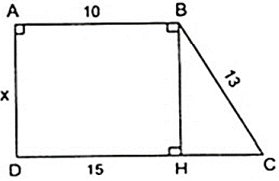
Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, cạnh đáy AB = 6cm và CD = 14cm.
Kẻ AH ⊥ CD, BK ⊥ CD thì AH//BK nên hình thang ABKH có hai cạnh bên song song.
Áp dụng tính chất của hình thang ABKH có hai cạnh bên song song, ta có:
Áp dụng định lí Py – ta – go vào tam giác ADH vuông tại H ta được:
Vậy chiều cao của hình thang cân là 3cm.
Câu 63:
Tính chiều cao BH của hình thang cân ABCD, biết AC ⊥ BD và hai cạnh đáy AB = a, CD = b. Từ đó suy ra cách vẽ hình.
Kẻ Bx ⊥ BD cắt DC tại E, do cùng với vuông góc với BD.
Hình thang ABEC có hai cạnh bên song song, nên AC = BE ( 1 ) và hai đáy AB = CE = a.
Suy ra DE = DC + CE = a + b
Lại có: AC = BD (vì là đường chéo của hình thang cân) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra BD = BE nên tam giác BDE vuồn cân tại B.
Do BH vừa là đường cao vừa là đường trung tuyến của tam giác BDE, nên
Lúc đó tam giác BDH vuông cân tại H.
Vậy BH = (a + b)/2.
Cách vẽ hình:
+ Bước 1: Vẽ Δ BDE vuông cân tại B có đường cao BH và DE = a + b.
+ Bước 2: Kẻ Bx//DE. Lấy C ∈ HE sao cho CE = b.
+ Bước 3: Kẻ Cy//DE cắt Bx tại A. Ta được hình thang thỏa mãn yêu cầu bài cho.
Câu 64:
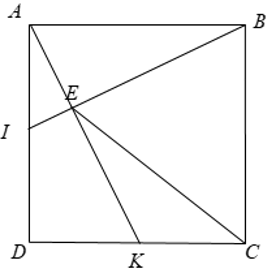
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC. Chứng minh rằng BI ⊥ AK.
Xét Δ BAI và Δ ADK có:
⇒ Δ BAI = Δ ADK ( c - g - c )
Câu 66:
Cho hai điểm A, B cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên d điểm M sao cho tổng MA + MB nhỏ nhất.
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d
Câu 67:
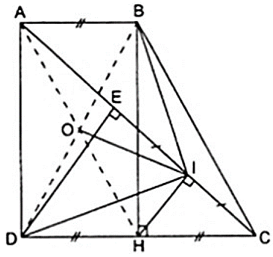
Cho hình thang vuông ABCD có và CD = 2AB. Kẻ DE ⊥ AC, gọi I là trung điểm của EC. Chứng minh rằng .
Vẽ BH ⊥ DC thì tứ giác ABHD có ba góc vuông là nên nó là hình chữ nhật.
Áp dụng tính chất về cạnh và giả thiết về hình chữ nhật ABHD ta được:
Lại có IE = IC ( 2 )
Từ ( 1 ), ( 2 ) suy ra HI là đường trung bình của tam giác DCE.
Áp dụng định lý về được trung bình trong tam giác DCE ta được HI//DE do DE ⊥ AC theo giả thiết nên HI ⊥ AC hay tam giác AIH vuông tại I.
+ Trong hình chữ nhật ABHD có
là đường trung tuyến của hai tam giác vuông AIH và BID.
Mặt khác ta lại có:
Điều đó chứng tỏ trong tam giác BID có IO là đường trung tuyến ứng với cạnh huyền và bằng nửa cạnh ấy nên nó là tam giác vuông tại I.
Vậy
Câu 68:
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN ⊥ AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng: AM = AN
Áp dụng định nghĩa và giả thiết của hình vuông ABCD ta được:
⇒ Δ ABM = Δ ADN( g - c - g )
Do đó AM = AN (cặp cạnh tương ứng bằng nhau)
Câu 69:
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN ⊥ AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng: Ba điểm B, I, D thẳng hàng.
Ta có IA, IC lần lượt là các đường trung tuyến ứng với cạnh huyền của hai tam giác vuông AMN, CMN.
Áp dụng tính chất đường trung tuyến ứng vói cạnh huyền của hai tam giác vuông trên và định nghĩa ta có:
Chứng tỏ hai điểm B và I cách đều hai điểm A và C nên BI là đường trung trực của đoạn AC.
Mà theo tính chất của hình vuông thì BD là đường trung trực của AC mà đoạn AC chỉ có một đường trung trực nên BI trung với BD hay B,I,D thẳng hàng.