Dạng 1. Tính số đo góc có đáp án
-
520 lượt thi
-
7 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
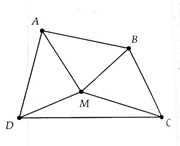
Cho tứ giác ABCD biết = 4:3:2:1.
a) Tính các góc của tứ giác ABCD.
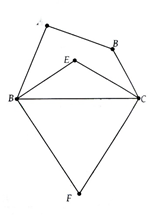
Câu 2:
b) Sử dụng tổng ba góc trong tam giác tính được .
Chú ý hai phân giác trong và ngoài tại mỗigóc của một tam giác thì vuông góc nhau, cùng với tổng bốn góc trong tứ giác, ta tính được
Câu 4:
Chứng minh rằng trong một tứ giác, tổng hai góc ngoài tại hai đỉnh bằng tổng hai góc trong tại hai đỉnh còn lại.
Trường hợp hai góc ngoài tại hai đỉnh kề nhau (h.1.5)
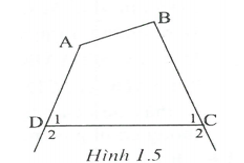
Gọi là số đo hai góc trong; , là số đo hai góc ngoài tại hai đỉnh kề nhau là C và D. Ta có:
. (1)
Xét tứ giác ABCD có: (2)
Từ (1) và (2) suy ra:
Trường hợp hai góc ngoài tại hai đỉnh đối nhau (h.1.6)
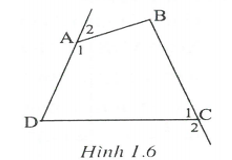
Chứng minh tương tự, ta được
Câu 5:
Cho tứ giác ABCD có . Các tia phân giác ngoài tại đỉnh C và D cắt nhau tại K. Tính số đo của góc CKD.
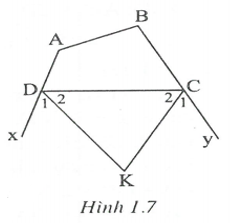
Ta có:
Do đó .
Xét có:
Câu 6:
Tứ giác ABCD có . Chứng minh rằng các đường phân giác của góc B và góc D song song với nhau hoặc trùng nhau.
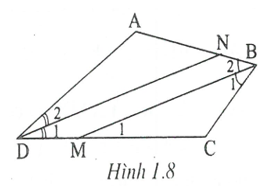
Xét tứ giác ABCD có:
Vì , nên (1)
Xét có (2)
Từ (1) và (2) suy ra . Do đó DN // BM.
Câu 7:
Cho tứ giác ABCD có . Tính số đo góc A, góc B.
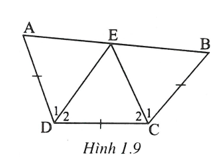
Vẽ đường phân giác của các góc và chúng cắt nhau tại E.
Xét có
(c.g.c)
(c.g.c)
Suy ra do đó ba điểm A, E, B thẳng hàng
Vậy . Do đó