Dạng 3.Tổng hợp có đáp án
-
547 lượt thi
-
11 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tứ giác ABCD có AB = AD, CB = CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).
a) Chứng minh AC là đường trung trực của BD.
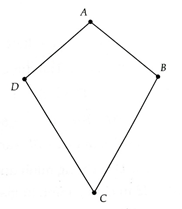
a) HS tự chứng minh
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Cho tứ giác ABCD có và BC = AD. Chứng minh:
a) ∆DAB = ∆CBA, từ đó suy ra BD = AC;Câu 9:
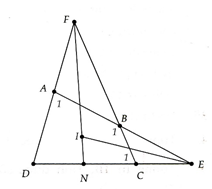
Cho tứ giác ABCD, AB Cắt CD tại E, BC cắt AD tại F. Các tia phân giác của và cắt nhau tại I. Chứng minh
a)
a) Gọi
Theo định lý về góc ngoài của tam giác
có ;
có ;
Vậy
DADE có
có
Thay vào (1) được (ĐPCM)Câu 11:
Coi mỗi người như một điểm, ta có chín điểm A, B, C,…
Nối hai điểm với nhau ta được một đoạn thẳng. Ta tô màu xanh nếu hai người không quen nhau, ta tô màu đỏ nếu hai người quen nhau. Ta sẽ chứng minh tồn tại một tứ giác có các cạnh và đường chéo cùng tô màu đỏ.
Trường hợp có một điểm là đầu mút của bốn đoạn thẳng màu xanh AB, AC, AD, AE vẽ nét đứt (h.1.17)

Xét có hai đoạn thẳng AB, AC màu xanh nên đoạn thẳng BC màu đỏ vì bất kì tam giác nào cũng có một đoạn thẳng màu đỏ. Tương tự các đoạn thẳng CD, DE, EB, BD, CE cũng có màu đỏ (vẽ nét liền) (h.1.18). Do đó tứ giác BCDE có các cạnh và đường chéo được tô đỏ nghĩa là tồn tại một nhóm bốn người đôi một quen nhau.
- Trường hợp mọi điểm đều là đầu mút của nhiều nhất là ba đoạn thẳng màu xanh. Không thể mọi điểm đều là đầu mút của ba đoạn thẳng màu xanh vì khi đó số đoạn thẳng màu xanh là .
Như vậy tồn tại một điểm là đầu mút của nhiều nhất là hai đoạn thẳng màu xanh, chẳng hạn đó là điểm A, do đó A là đầu mút của ít nhất là sáu đoạn thẳng màu đỏ, giả sử đó là AB, AC, AD, AE, AF, AG (h.1.19)
Trong sáu điểm B, C, D, E, F, G tồn tại ba điểm là đỉnh của một tam giác có ba cạnh cùng màu (đây là bài toán cơ bản về phương pháp tô màu) chẳng hạn đó là (h.1.20).

Trong có một cạnh màu đỏ (theo đề bài) nên ba cạnh của cùng màu đỏ. Khi đó tứ giác ABCD là tứ giác có các cạnh và đường chéo được tô đỏ, nghĩa là tồn tại một nhóm bốn người đôi một quen nhau.
