Dạng 1. Chứng minh hai điểm hoặc hai hình đối xứng với nhau qua một điểm có đáp án
-
607 lượt thi
-
2 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC. Gọi các điểm D, E theo thứ tự là trung điểm của AB và AC. Lấy P đối xứng vói B qua tâm E và Q đối xứng với qua tâm D. Chứng minh rằng hai điểm P, Q đối xứng với nhau qua tâm A.
Xem đáp án
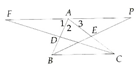

Ta có: BAPC và CAFB đều là hình bình hành
Vậy F,A,P thẳng hàng.
Câu 2:
Cho tứ giác ABCD. Gọi M, N, P, Q theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Gọi E là điểm bất kì nằm ngoài tứ giác, E là điểm đối xứng với E qua M, G là điểm đối xứng với E qua Q, H là điểm đối xứng với G qua P. Chứng minh rằng E là điểm đối xứng với H qua điểm N.
Xem đáp án
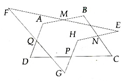

Ta có EBFA, FAGD, GDHC đều là hình hành. Vậy BECH cũng là hình bình hành.
Vậy E đối xứng với H qua N.
