Dạng 2. Sử dụng tính chất đối xứng trục để giải toán có đáp án
-
575 lượt thi
-
3 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC. Gọi E, F theo thứ tự là trung điểm của các cạnh AB và AC. Một điểm M bất kì thuộc cạnh BC, có điểm đối xứng vói M qua điểm F là Q và điểm đối xứng của M qua điểm F là Q. Chứng minh:
a) A thuộc đường thẳng PQ;
Xem đáp án
a) Ta chứng minh được A thuộc đường thẳng PQ
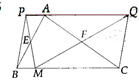
Câu 2:
b) BCQP là hình bình hành.
Xem đáp án
b) Ta có:
PA//BM,PA= BM
AQ//MC, AQ = MC
Suy ra BCQP là hình bình hành
Câu 3:
Cho hình bình hành ABCD. Trên cạnh AD lấy điểm E và trên cạnh CB lấy điểm E sao cho AE = CF. Chứng minh rằng hai điểm E, F đối xứng với nhau qua giao điểm của các đường chéo AC, BD.
Xem đáp án
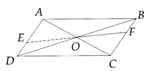
Ta có AEFC là hình bình hành (AE//FC; AE = CF) => đường EF cắt AC tại trung điểm O của AC => nên E,O, F thẳng hàng và O cũng là trung điểm của EF (ĐPCM).